Theoretical Model: Condorcet's Jury Theorem, Part 1

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
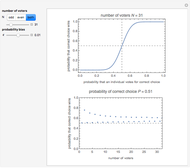
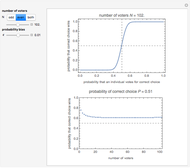
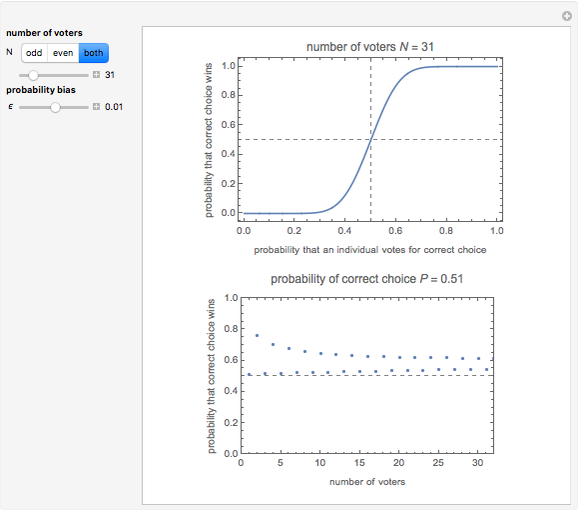
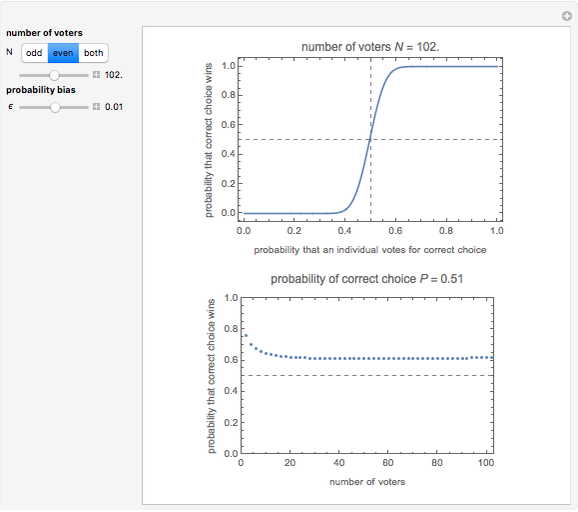
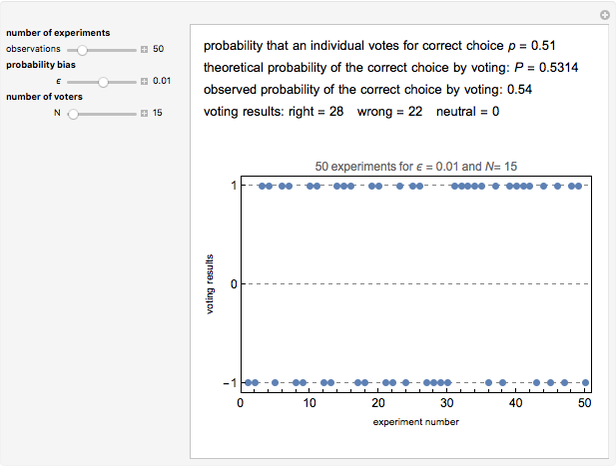
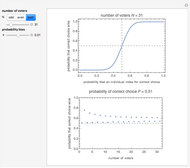
This is the first of five Demonstrations about Condorcet's jury theorem (1785). It uses the formula  , where the probability
, where the probability  and
and  is the number of voters. The theorem states if the voters are independent and each has probability
is the number of voters. The theorem states if the voters are independent and each has probability 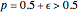 of voting for the correct choice, then the probability
of voting for the correct choice, then the probability  of the majority voting for the correct choice is larger than
of the majority voting for the correct choice is larger than  and converges to one as the population
and converges to one as the population  goes to infinity.
goes to infinity.
Contributed by: Tetsuya Saito (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Condorcet's jury theorem (CJT) is one of the most fundamental theorems in voting theory and related fields. Suppose a community of  independent voters faces a yes/no decision on which there is some correct or best choice, and each voter has probability
independent voters faces a yes/no decision on which there is some correct or best choice, and each voter has probability  of making the correct choice individually. If
of making the correct choice individually. If  is the probability that a majority of the community makes the correct choice, then if
is the probability that a majority of the community makes the correct choice, then if  ,
,  .
.
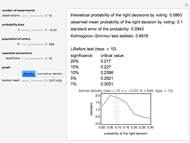
The proof of the theorem is easy (i.e., by induction) and the formula for 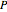 is also well known (see the formula in the caption). In a series of five Demonstrations, of which this is the first, we try to see and confirm this theorem from various viewpoints using numerical simulations. In this Demonstration we show the theoretical characteristics of the model in terms of the probability bias defined by
is also well known (see the formula in the caption). In a series of five Demonstrations, of which this is the first, we try to see and confirm this theorem from various viewpoints using numerical simulations. In this Demonstration we show the theoretical characteristics of the model in terms of the probability bias defined by  and number of voters
and number of voters  . We show how quickly (or slowly) the probability converges and how odd and even population sizes affect the theoretical results. In these Demonstrations, neutral decisions in which the votes are divided evenly are assumed to be correct decisions.
. We show how quickly (or slowly) the probability converges and how odd and even population sizes affect the theoretical results. In these Demonstrations, neutral decisions in which the votes are divided evenly are assumed to be correct decisions.
References:
H. Abdi and P. Molin, "Lilliefors/Van Soest's Test of Normality," in Encyclopedia of Measurement and Statistics (N. Salkind, ed.), Thousand Oaks, CA: SAGE Publications, 2007.
Marquis de Condorcet, "Essai sur l'Application de l'Analyse à la Probabilité des Décisions Rendues à la Pluralité des Voix (Essay on the Application of Analysis to the Probability of Majority Decisions)," 1785.
Permanent Citation