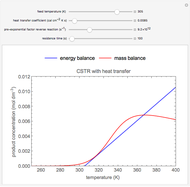
Thermodynamic Properties of Acetylene Using Cubic Equations of State

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Any thermodynamic property, 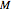 , can be expressed as the sum of an ideal gas contribution and a residual non-ideal contribution:
, can be expressed as the sum of an ideal gas contribution and a residual non-ideal contribution:  , where
, where 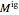 and
and 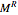 are the ideal gas and residual contributions, respectively. For a given equation of state, the residual contribution can then be expressed as a function of
are the ideal gas and residual contributions, respectively. For a given equation of state, the residual contribution can then be expressed as a function of 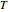 ,
, 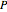 , and compressibility factor
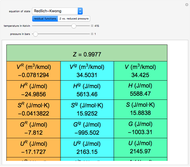
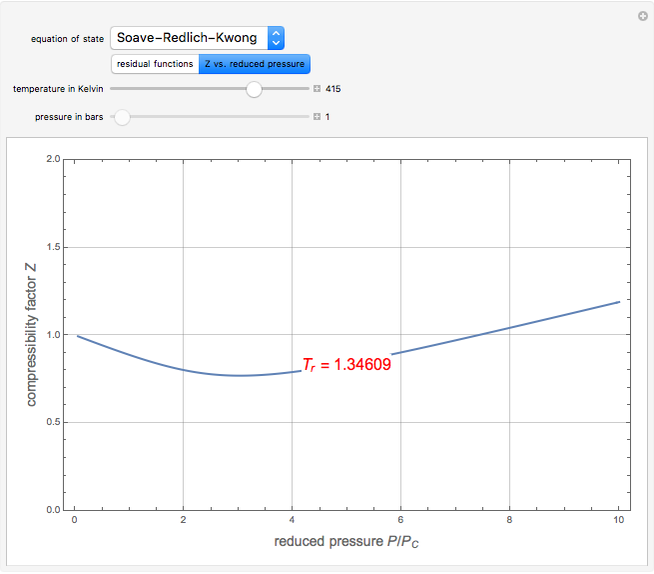
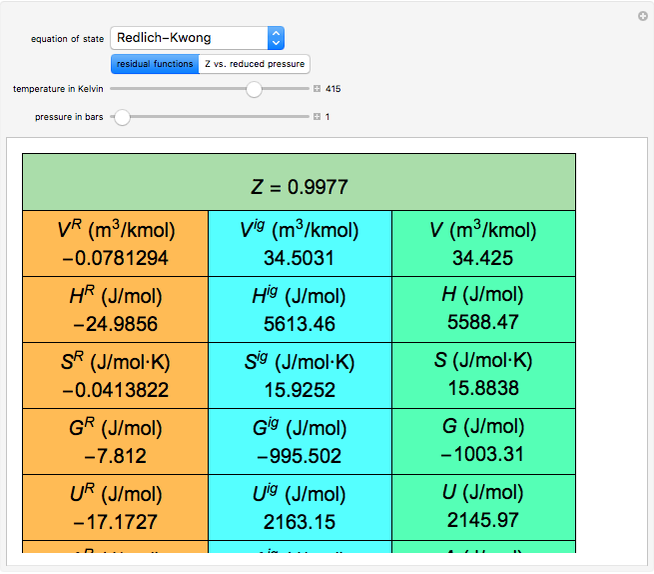
, and compressibility factor 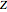 . In this Demonstration, the compressibility factor for a single gas chemical species (acetylene) is computed, from which the enthalpy (
. In this Demonstration, the compressibility factor for a single gas chemical species (acetylene) is computed, from which the enthalpy ( in
in 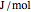 ) and entropy (
) and entropy (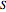 in
in 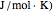 can be determined for given
can be determined for given 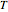 and
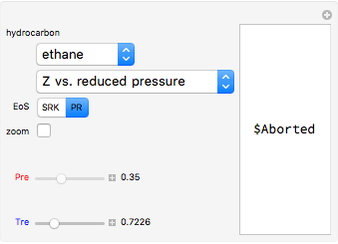
and  . You can select from one of three cubic equations of state (Redlich–Kwong, Soave–Redlich–Kwong, or Peng–Robinson) as well as the temperature (in
. You can select from one of three cubic equations of state (Redlich–Kwong, Soave–Redlich–Kwong, or Peng–Robinson) as well as the temperature (in 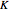 ) and the pressure (in
) and the pressure (in 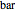 ). The reference state is taken an ideal gas at
). The reference state is taken an ideal gas at 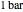 and
and 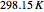 . This information is then used to obtain the molar volume (in
. This information is then used to obtain the molar volume (in 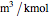 ) as well as additional thermodynamics properties such as the Gibbs free energy (
) as well as additional thermodynamics properties such as the Gibbs free energy ( in
in 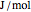 ), Helmholtz free energy (
), Helmholtz free energy (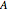 in
in 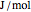 ), and internal energy (
), and internal energy (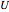 in
in  ). In addition,
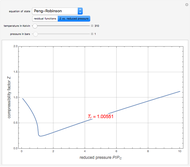
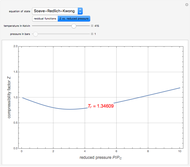
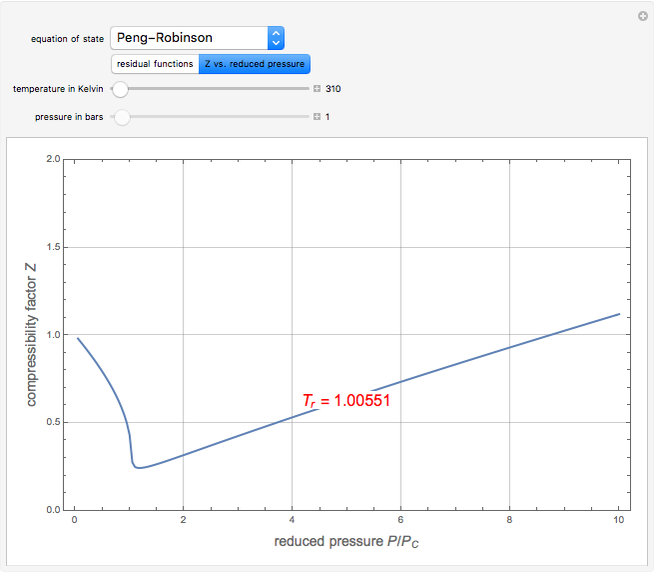
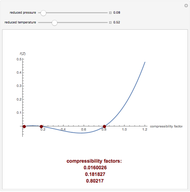
). In addition, 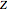 is plotted versus reduced pressure
is plotted versus reduced pressure 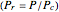 for a user-specified reduced temperature (
for a user-specified reduced temperature (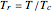 ), where
), where  and
and  are the critical pressure and temperature for acetylene. For an ideal gas
are the critical pressure and temperature for acetylene. For an ideal gas  .
.
Contributed by: Housam Binous and Brian G. Higgins (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] J. M. Smith, H. C. Van Ness, and M. M. Abbott, Introduction to Chemical Engineering Thermodynamics, 7th ed., New York: McGraw-Hill, 2005.
Permanent Citation
"Thermodynamic Properties of Acetylene Using Cubic Equations of State"
http://demonstrations.wolfram.com/ThermodynamicPropertiesOfAcetyleneUsingCubicEquationsOfState/
Wolfram Demonstrations Project
Published: November 10 2011