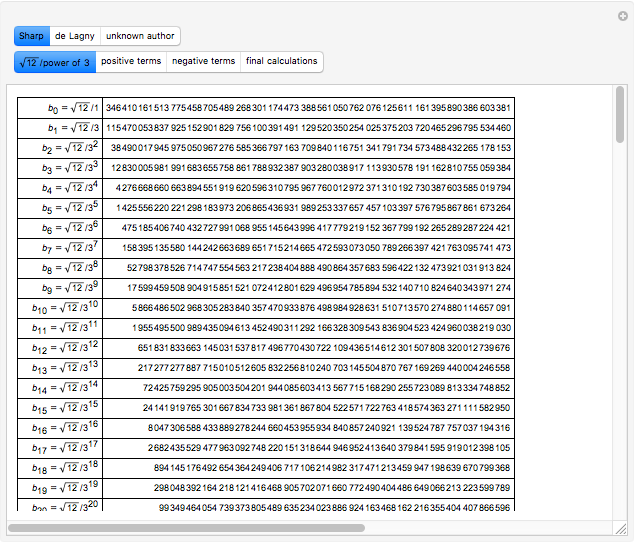
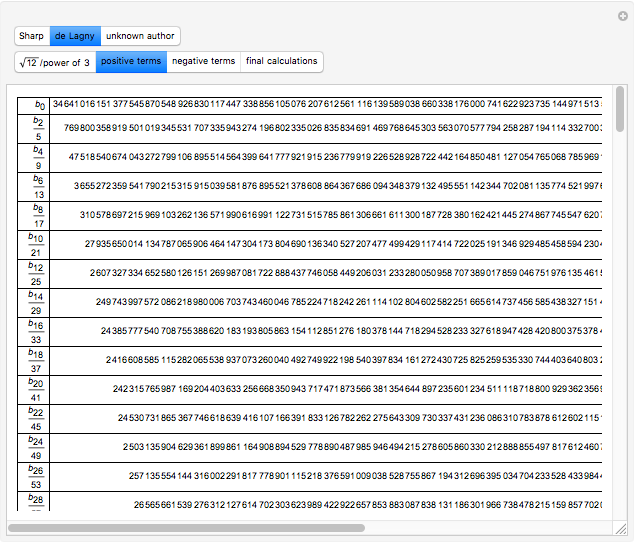
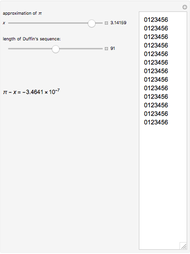
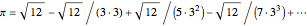Three Calculations of Pi Before 1800

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
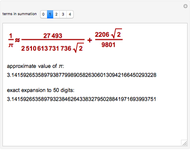
This Demonstration shows three calculations of  using the Gregory–Leibniz series
using the Gregory–Leibniz series 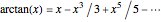 with
with 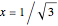 .
.
Contributed by: Izidor Hafner (June 2016)
Open content licensed under CC BY-NC-SA
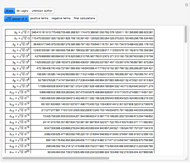
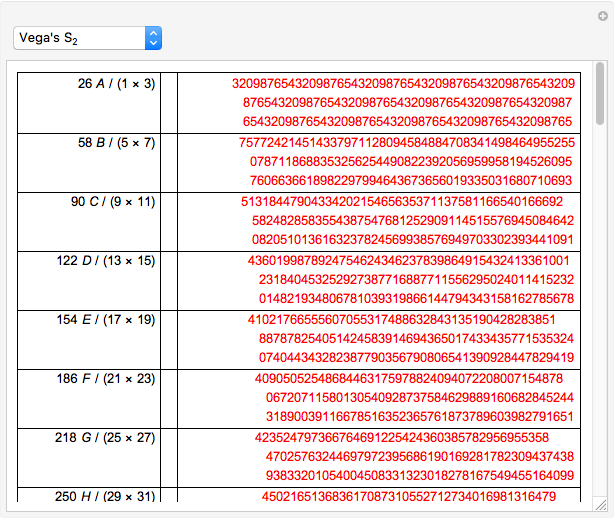
Snapshots
Details
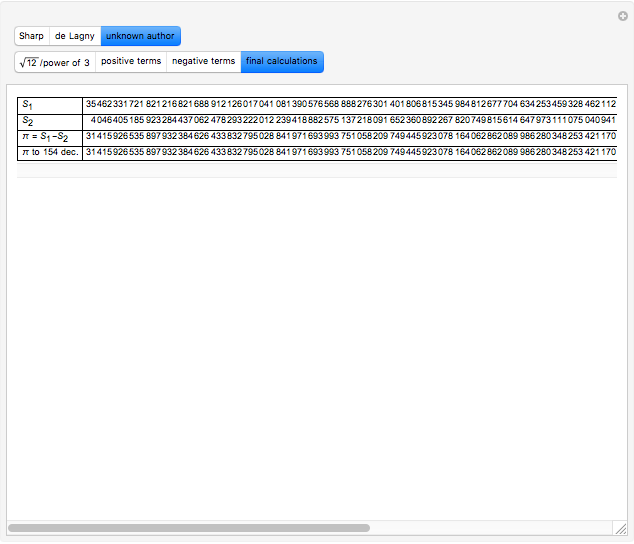
According to [1, pp. 356–357], in 1699 Sharp used the Gregory series with 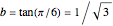 to determine an approximation of
to determine an approximation of  to 72 decimal places (71 were correct). De Lagny, in 1706, went to 127 places (112 correct) using the same series.
to 72 decimal places (71 were correct). De Lagny, in 1706, went to 127 places (112 correct) using the same series.
Toward the end of the eighteenth century, F. X. von Zach saw a manuscript by an unknown author in the Radcliffe Library, Oxford, which gives the value of  to 154 places (152 correct) [2].
to 154 places (152 correct) [2].
In this Demonstration, we suppose that those mathematicians calculated values of terms to two or three decimals more than the reported results.
References
[1] W. W. Rouse Ball and H. S. M. Coxeter, Mathematical Recreations and Essays, 13th ed., New York: Dover Publications, 1987.
[2] B. Wardhaugh, "A ‘Lost’ Chapter in the Calculation of π: Baron Zach and MS Bodleian 949," Historia Mathematica, 42(3), 2015 pp. 343–351. doi:10.1016/j.hm.2015.01.002.
Permanent Citation