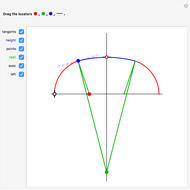
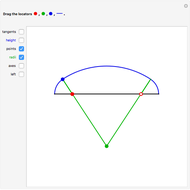
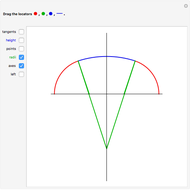
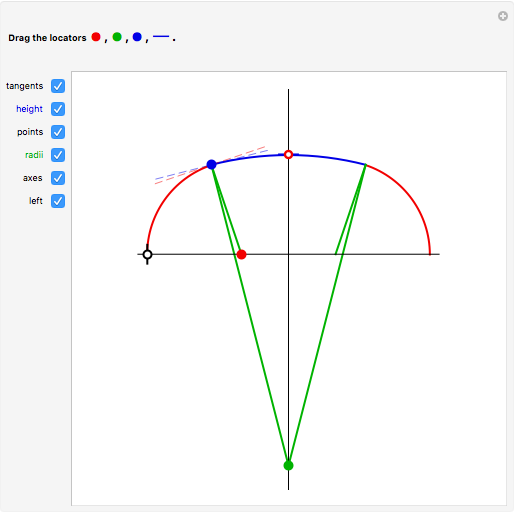
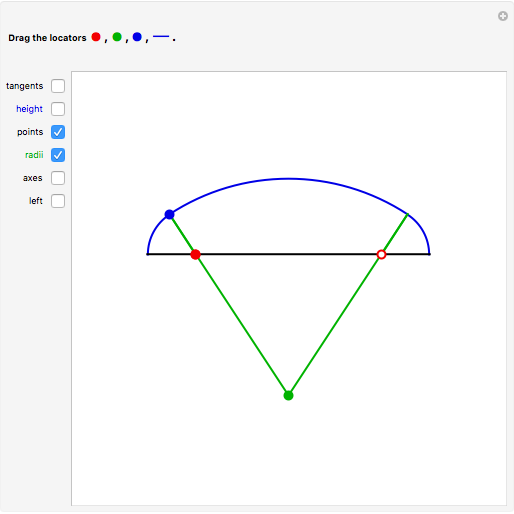
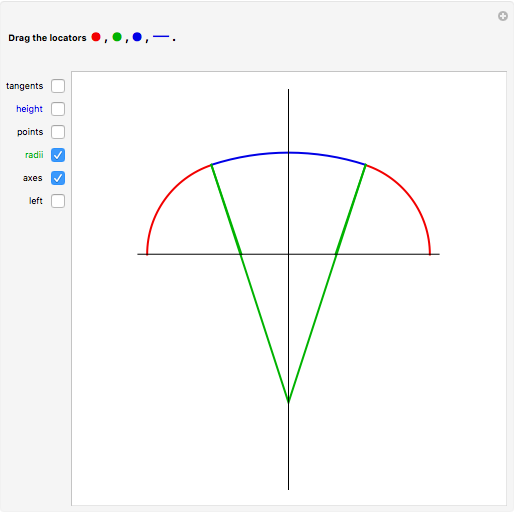
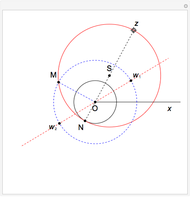
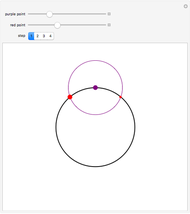
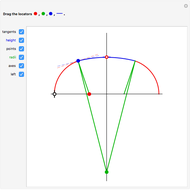
A three-centered arch consists of three segments of circles smoothly "glued" together. In this Demonstration you can choose to show a black line on the left axis to mark the width of the arch using the checkbox "left". You can mark and move a target height of the arch using the blue segment ("height"). Then you can select different positions of the red, green, and blue locators to reach this marked height. When you select approximately correct parameters, little red circles appear at the top of the arch (when the arch touches the blue marker at the top) and also on the right part of the axis (when the two green lines there overlap). If the tangents are identical, then the segments of the circles join smoothly.