Three-Element Viscoelastic Models

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
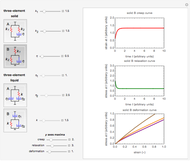
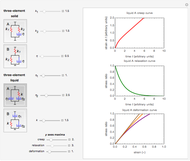
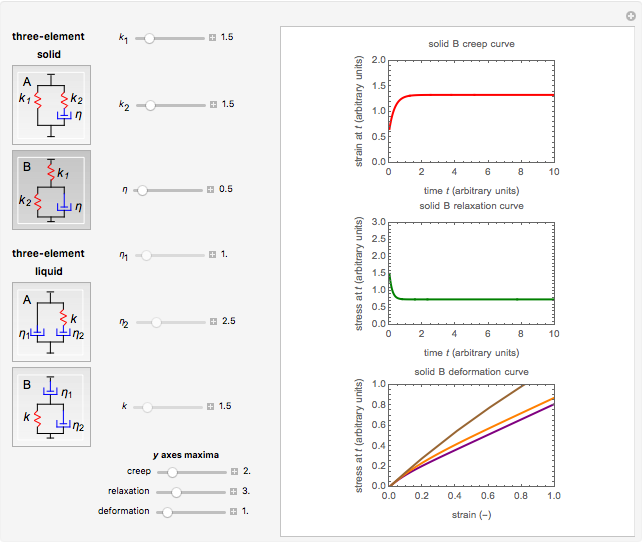
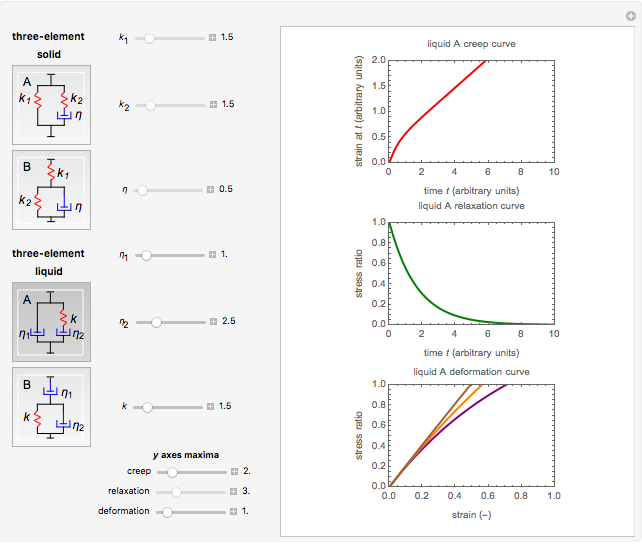
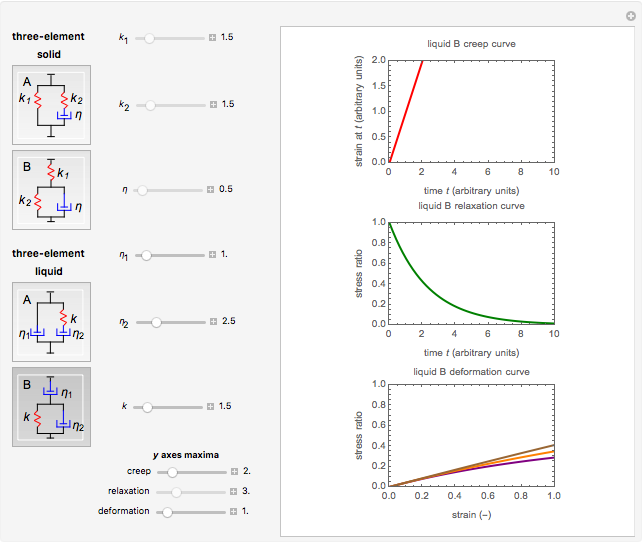
This Demonstration plots ideal creep, stress-relaxation, and stress-strain curves of a viscoelastic solid or liquid represented by a three-element mechanical analog. The solid model comes in the form of either a spring and Maxwell element in parallel or a spring and a Kelvin–Voigt element in series, and the liquid is in the form of a dashpot and a Maxwell element in parallel or a dashpot and a Kelvin–Voigt element in series. The creep curve is generated for a unit-step stress, the relaxation curve for a unit-step strain, and the stress-strain curves for three constant strain rates (.5, 1.0, and 5.0 arbitrary time unit reciprocal). The Demonstration shows that the curves produced by each model's two versions, with the same spring constants and dashpots' viscosities, are quantitatively different, although they are qualitatively similar.
Contributed by: Mark D. Normand and Micha Peleg (February 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: solid model B
Snapshot 2: liquid model A
Snapshot 3: liquid model B
Mathematical models of linear viscoelasticity are frequently presented and explained using a mechanical analog composed of springs and dashpots. The three-element solid array, having two springs and a dashpot, is the simplest analog that exhibits realistic creep, relaxation, and straining, at least qualitatively. The same can be said about the three-element liquid model composed of two dashpots and a spring. The solid models can be presented in two forms: a spring and a Maxwell element in parallel (type A) or a spring and a Kelvin–Voigt element in series (type B). The liquid models also can be presented in two forms: a dashpot and a Maxwell element in parallel (type A) or a dashpot and a Kelvin–Voigt element in series (type B). (The Maxwell element has a spring and a dashpot in series and the Kelvin–Voigt in parallel.) The mechanical analog lets you visualize the solution of the model's (differential) constitutive equation, especially for creep and stress-relaxation.
The constitutive equation of the type A three-element solid model is 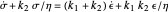 and that of type B is
and that of type B is 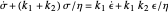 , where
, where 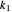 and
and 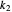 are the springs' constants, in our case in arbitrary stress units, and
are the springs' constants, in our case in arbitrary stress units, and  is the dashpot's viscosity, in arbitrary stress times time units.
is the dashpot's viscosity, in arbitrary stress times time units.
The constitutive equation of the type A three-element liquid model is 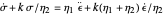 and that of type B is
and that of type B is 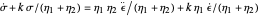 , where
, where 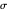 is the stress,
is the stress, 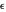 is the strain,
is the strain, 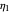 and
and 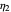 are the dashpots' viscosities, (in our case in arbitrary stress times time units), and
are the dashpots' viscosities, (in our case in arbitrary stress times time units), and  is the spring's constant in arbitrary stress units.
is the spring's constant in arbitrary stress units.
Both versions of each model have the same general form 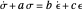 or
or 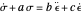 and hence can be used interchangeably after rearrangement of the constants. The generated creep curve, strain versus time, is the solution of the constitutive equation for a step-stress loading, and the stress-relaxation curve for a step-strain loading. Each generated stress-strain relationship is for constant strain-rate deformation where the strain
and hence can be used interchangeably after rearrangement of the constants. The generated creep curve, strain versus time, is the solution of the constitutive equation for a step-stress loading, and the stress-relaxation curve for a step-strain loading. Each generated stress-strain relationship is for constant strain-rate deformation where the strain  .
.
In this Demonstration, you can select the magnitudes of either 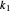 ,
, 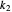 and
and  or
or 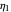 ,
, 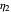 and
and  with sliders. The program calculates and plots the corresponding creep, stress-relaxation, and stress-strain curves for three constant strain rates .5, 1.0, and 5.0 arbitrary time reciprocal.
with sliders. The program calculates and plots the corresponding creep, stress-relaxation, and stress-strain curves for three constant strain rates .5, 1.0, and 5.0 arbitrary time reciprocal.
The plots' 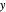 axis scale maxima can also be entered with sliders for improved resolution.
axis scale maxima can also be entered with sliders for improved resolution.
Reference
[1] D. R. Bland, The Theory of Linear Viscoelasticity, New York: Pergamon Press, 1960.
Permanent Citation