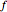Three Vector Spaces

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
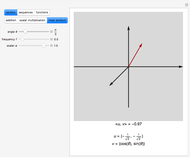
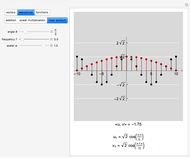
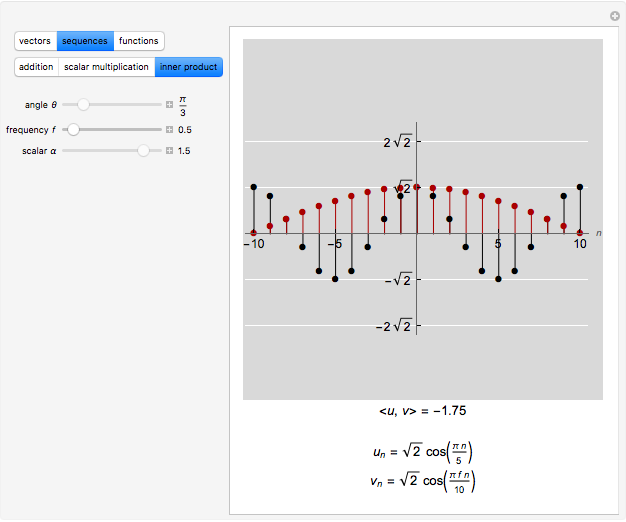
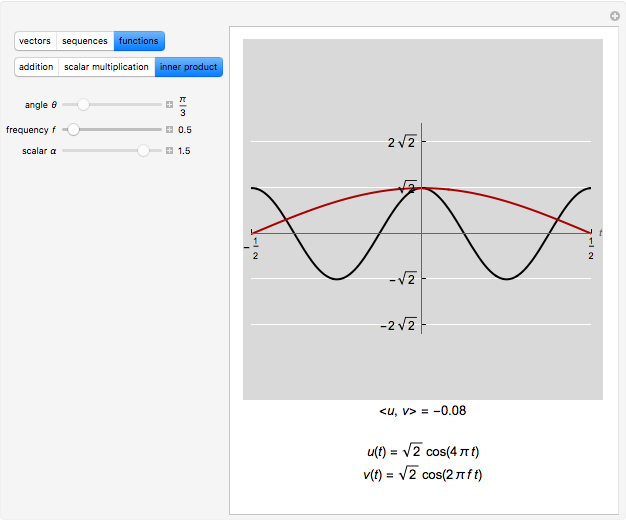
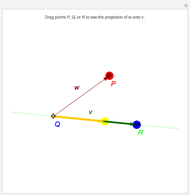
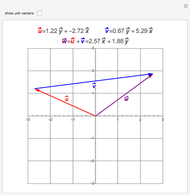
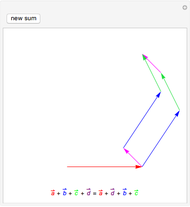
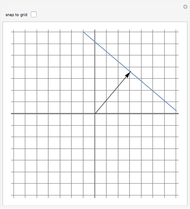
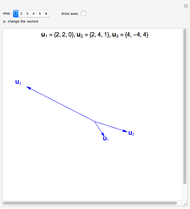
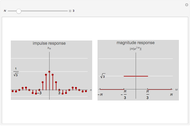
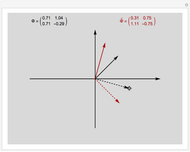
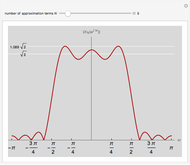
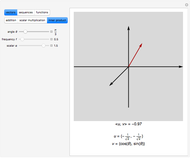
This Demonstration shows addition and scalar multiplication on vectors in three vector spaces: 2D vectors, sequences, and functions. A vector space becomes an inner-product space with an inner product. In particular, the intuitive notion of orthogonality for 2D vectors, when the inner product equals 0, is shown in the possibly unintuitive settings of sequences and functions.
[more]
Contributed by: Jelena Kovacevic (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A vector space is a set of objects, called vectors, with two operations, addition and scalar multiplication (that satisfy certain properties). While the notion of a vector space is intuitive in standard Euclidean spaces, it may not be when vectors are other objects, such as functions or sequences. We can add functions, resulting in a function. We can multiply functions by scalars, again resulting in a function. With an appropriate inner product, a vector space becomes an inner-product space. We can then define orthogonality as we do for standard vectors in the real plane: two vectors (sequences or functions) are orthogonal when their inner product equals 0.
In this Demonstration, we consider 2D vectors, sequences on an interval, and functions on an interval. The inner products are defined as follows:
For vectors, 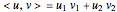 .
.
For sequences, 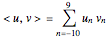 .
.
For functions,  .
.
Reference
[1] M. Vetterli, J. Kovačević, and V. K. Goyal, Foundations of Signal Processing, Cambridge: Cambridge University Press, 2014. www.fourierandwavelets.org.
Permanent Citation