Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

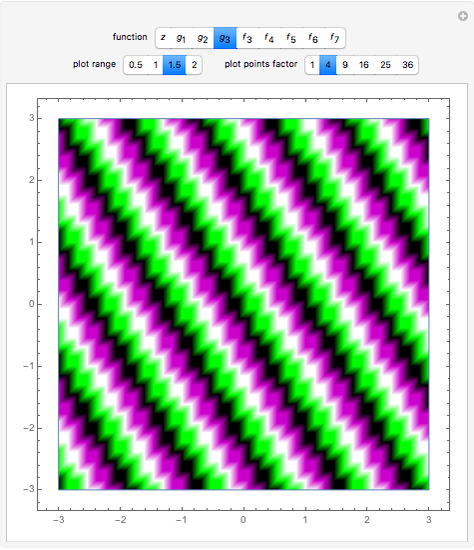
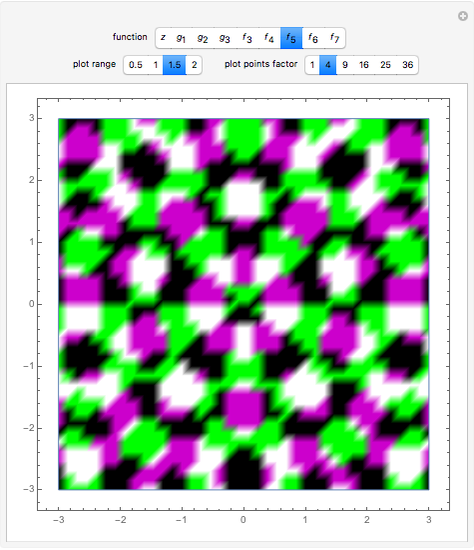
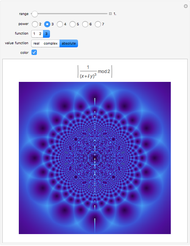
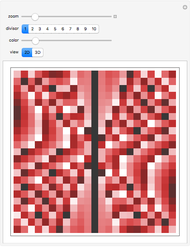
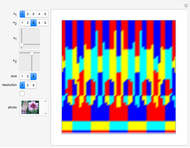
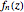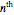Threefold Symmetry from Rotated Plane Waves

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

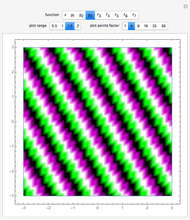
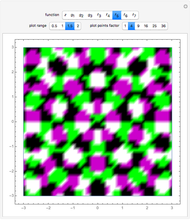
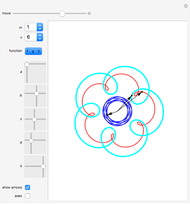
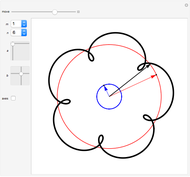
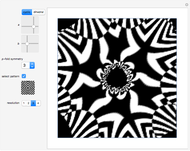
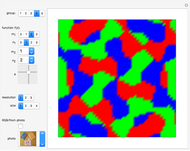
The plot of the function represents a plane wave periodic in the direction of the imaginary axis. Threefold symmetry is created by taking the mean of the functions , , 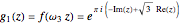and 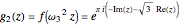, where 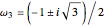are the two complex roots of the equation 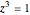. So is invariant under rotation by ; in other words, it has threefold symmetry.

[more]

Similarly, has -fold symmetry for , using the roots of unity, the solutions of .

[less]

Contributed by: Izidor Hafner (February 2016)
Open content licensed under CC BY-NC-SA

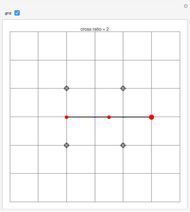
Snapshots

Details

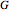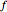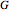If is a finite group of transformations in the complex plane with elements, and is a function defined on the complex plane, the average of over is

.

The cyclic group 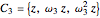corresponds to the case .

Reference

[1] F. A. Farris, Creating Symmetry, The Artful Mathematics of Wallpaper Patterns, Princeton: Princeton University Press, 2015 pp. 66-67.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send