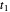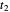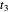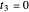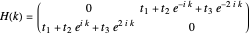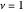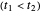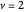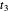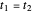Topological Winding Number in 1D Su-Schrieffer-Heeger Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
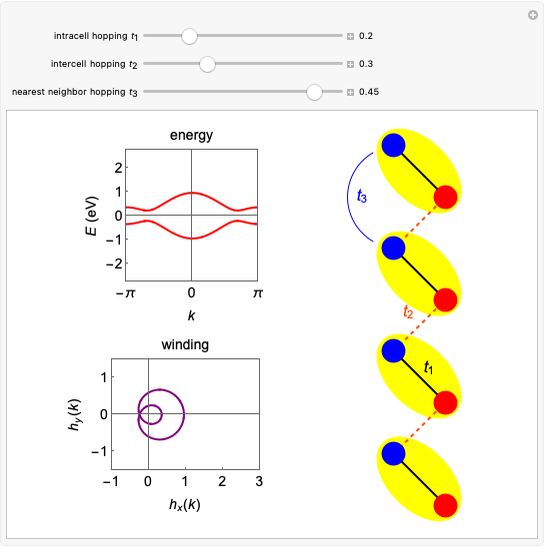
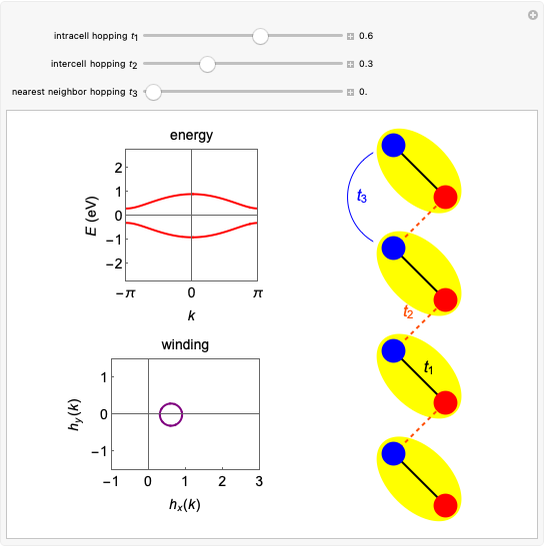
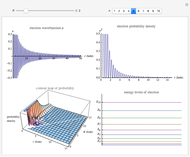
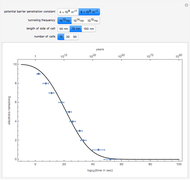
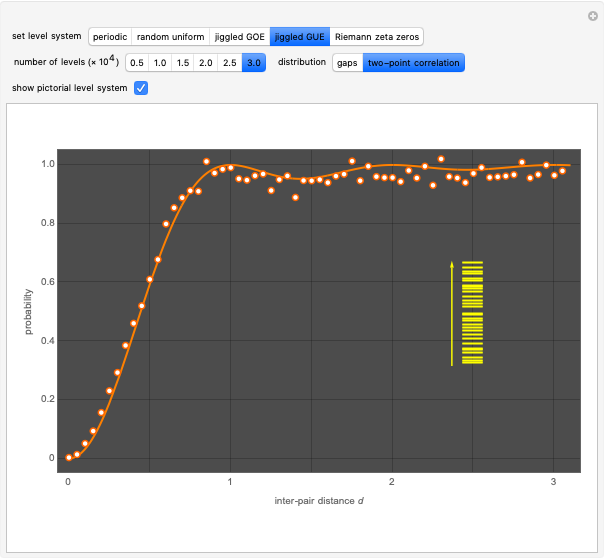
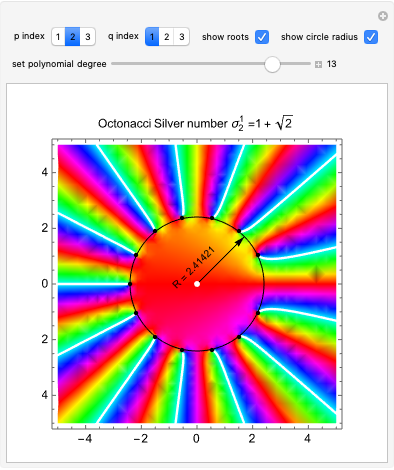
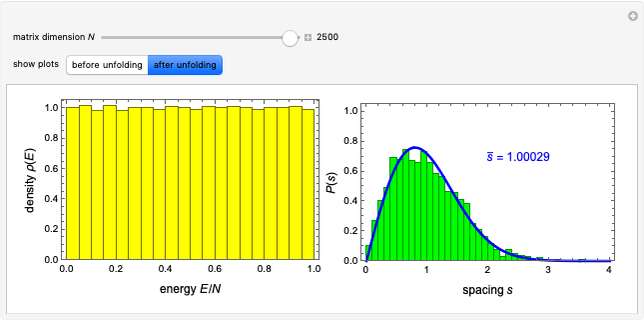
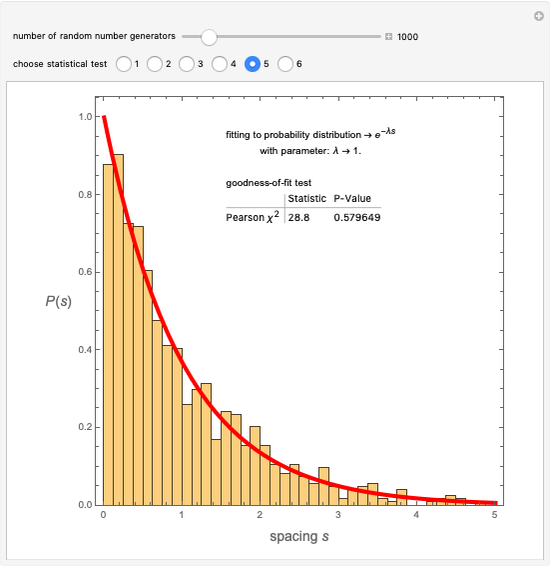
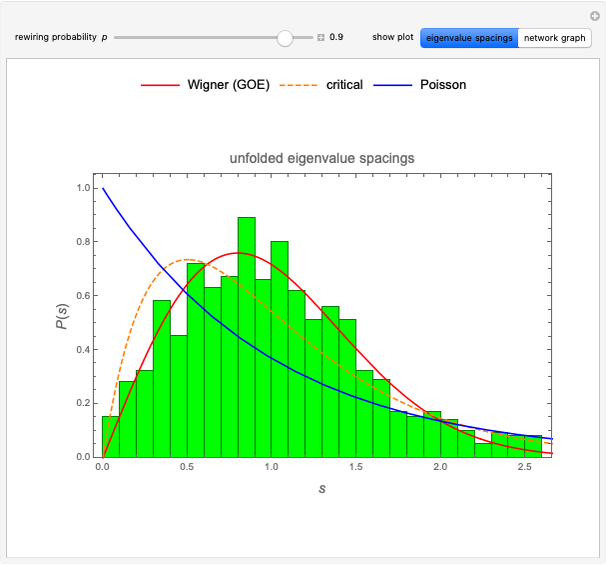
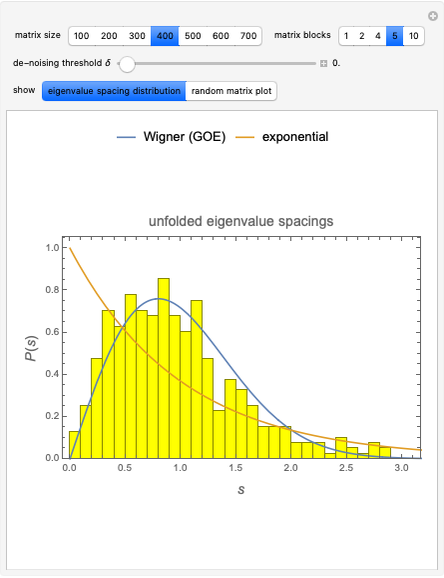
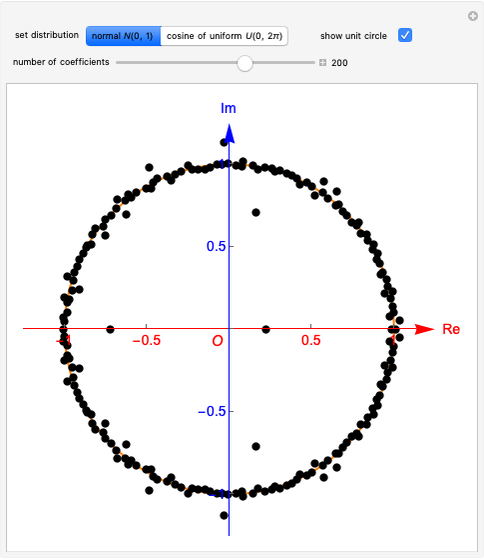
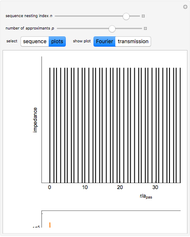
This Demonstration shows the electronic energy dispersion relation and the winding of the Hamiltonian in the Brillouin zone (BZ) of the extended one-dimensional (1D) Su–Schrieffer–Heeger (SSH) tight-binding model. The SSH model is often used as a parametric toy model for explaining the appearance of topological insulating phases in low-dimensional condensed matter systems such as polyacetylene chains. It is also often used as a pedagogical introduction to the more advanced topic of topological insulator 2D systems.
[more]
Contributed by: Jessica Alfonsi (September 2016)
Padova, Italy
Open content licensed under CC BY-NC-SA
Details
Snapshot 1: topological insulating phase: the circle in the winding plot encloses the origin of the BZ; winding number 
Snapshot 2: trivial insulating phase: the circle in the winding plot does not include the origin of the BZ; winding number 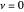
Snapshot 3: metallic phase: the circle in the winding plot crosses the origin of the BZ; winding number is undefined
Snapshot 4: trivial insulating phase and full dimerization limit due to dominating intracell hopping amplitude (winding plot reduces to a point off the origin)
Snapshot 5: topological insulating phase and full dimerization limit due to dominating intercell hopping amplitude
Snapshot 6: topological insulating phase with next-nearest neighbor hopping added to the SSH Hamiltonian, winding number 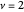
References
[1] J. K. Asbóth, L. Oroszlány and A. Pályi, A Short Course on Topological Insulators, Cham, Switzerland: Springer International Publishing, 2016. doi:10.1007/978-3-319-25607-8. Pre-print available at arxiv.org/abs/1509.02295.
[2] L. Li, C. Yang and S. Chen, "Winding Numbers of Phase Transition Points for One-Dimensional Topological Systems," Europhysics Letters, 112(1), 2015 10004. iopscience.iop.org/0295-5075/112/1/10004.
Snapshots
Permanent Citation