Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Total Areas of Alternating Subtriangles in a Regular Polygon with 2n Sides

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

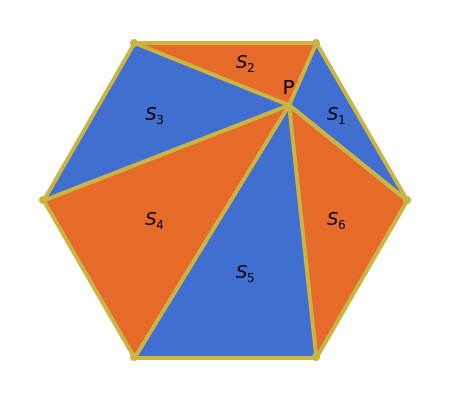
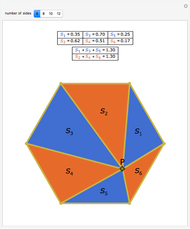
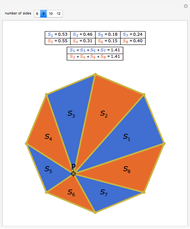
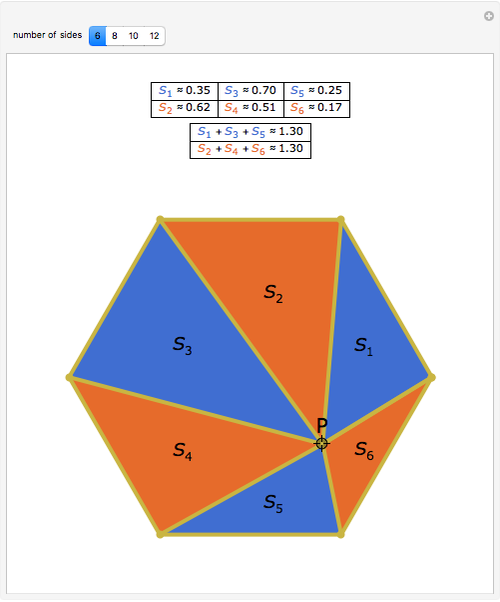
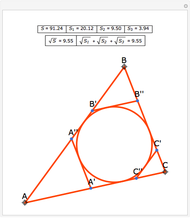
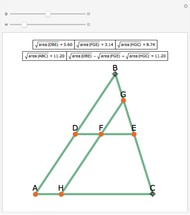
Let P be a point connected to and inside the vertices of a polygon with 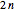sides. Number the triangles counterclockwise from 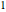to . Then the sum of the areas of the even-numbered triangles is equal to the sum of the areas of the odd-numbered triangles.

[more]

Drag the point P to change the figure.

[less]

Contributed by: Jay Warendorff (January 2009)
Open content licensed under CC BY-NC-SA

Snapshots

Details

A generalization of problem 4.28 in Problems in Plane and Solid Geometry v.1 Plane Geometry by Viktor Prasolov.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send