Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Total Probability and Bayes's Theorem

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

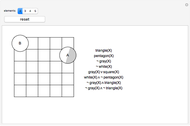
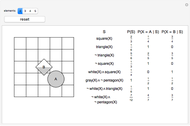
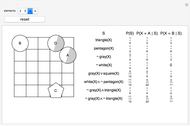
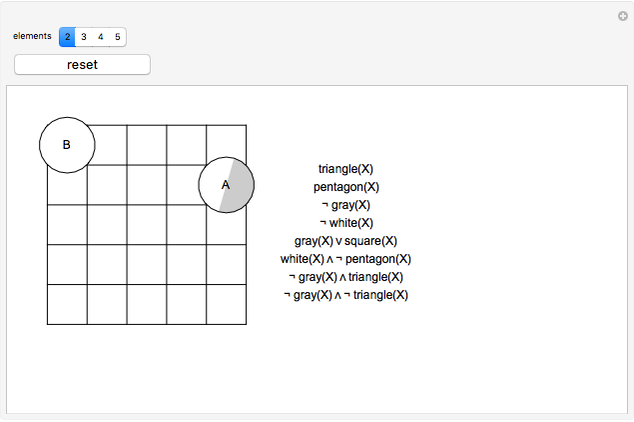
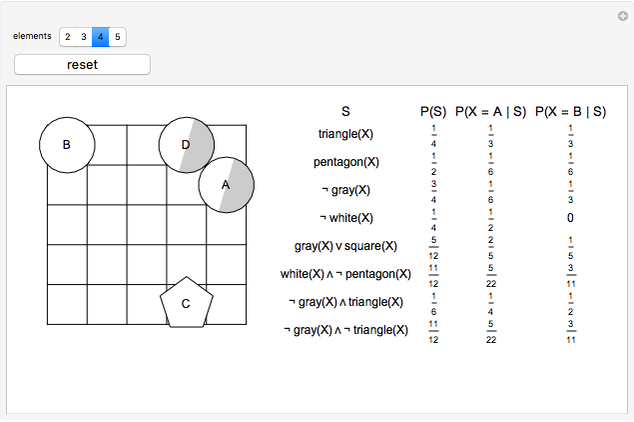
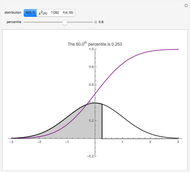
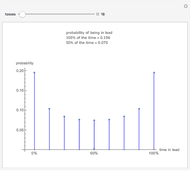
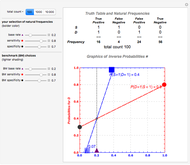
This Demonstration provides examples of total probability and Bayes's theorem. In the given world a figure X is randomly chosen. What is the probability of the given statement S? Suppose the statement is true. What is the probability that X = A? What is the probability that X = B?

[more]

If the probability of S is 0, the conditional probability P(X=A|S) is undefined (or undecided, denoted by U).

A simple two-dimensional area is occupied by white or gray triangles, squares, and pentagons. A disk means that the shape of the element is not known; in such a case a proposition of type Shape() has probability 1/3. A gray-white figure means that the color of the figure is not known; in such a case a proposition of type Color(x) has probability 1/2.

[less]

Contributed by: Izidor Hafner (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The conditional probability of an event A assuming that B has occurred, denoted P(A|B), equals P(A|B)=(P(A ⋂ B))/(P(B)). If P(B)=0, P(A|B) is undefined.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send