Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Toy Model of an Inflating Wormhole

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

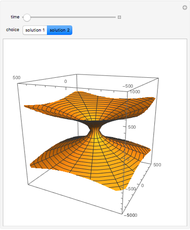
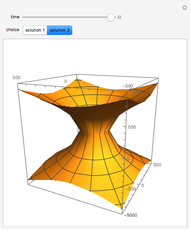
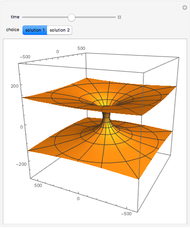
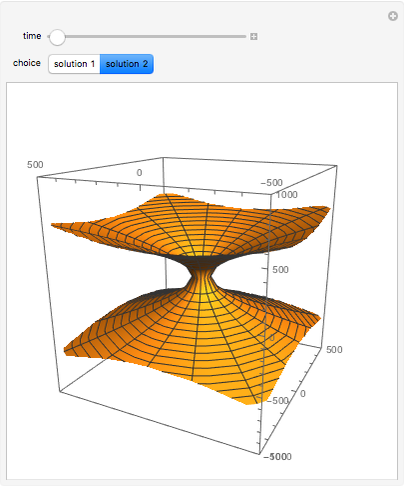
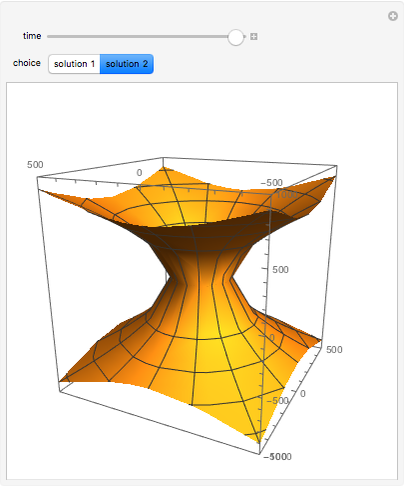
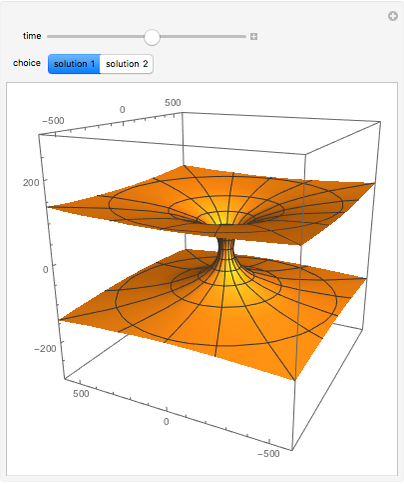
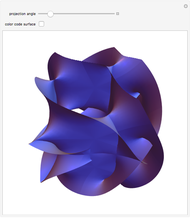
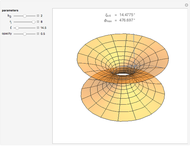
There is a possibility that the laws of quantum field theory and general relativity might allow for the existence of wormholes. These can be thought of as "bridges" connecting two otherwise distant regions of space. It is unknown if negative energy in a quantity required to support macroscopic transversable wormholes exists. Spatial hypersurfaces are shown to illustrate the change in size of the wormhole with time through embedding diagrams.

Contributed by: Enrique Zeleny (March 2011)
Based on work by: Thomas A. Roman
Open content licensed under CC BY-NC-SA

Snapshots

Details

The metric is spherically symmetric, static and transversable in the sense introduced by Morris and Thorne, with an exponential deSitter scale factor multiplying the spatial part

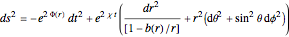, where:

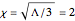— cosmological constant

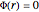— redshift function has no effect

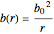— shape function choice 1

— shape function choice 2

— throat size

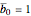— location of the throat

Coordinates with bar correspond to embedding space and "scale" exponentially with time.

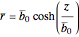— in terms of , embedding function in choice 1

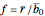— ensures that this ratio is time-independent in choice 1

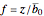— ensures that this ratio is time-independent in choice 2

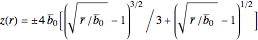— the usual "lift" function and embedding function in choice 2

T. Roman, "The Inflation Wormhole: A Mathematica Animation," Computers in Physics, 8(4), 1994 pp. 480.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send