Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Tracing a Cyclogon: Roulette of a Polygon Rolling along a Line

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

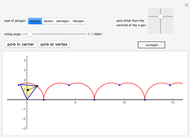
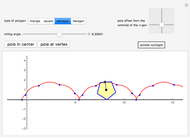
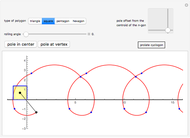
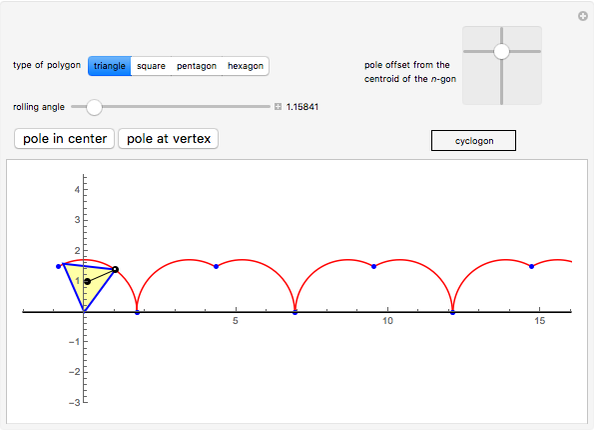
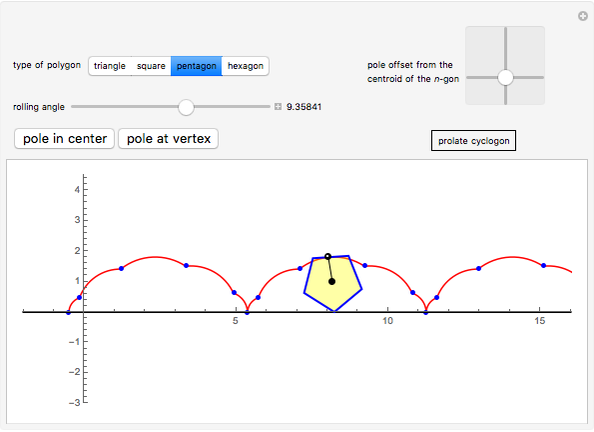
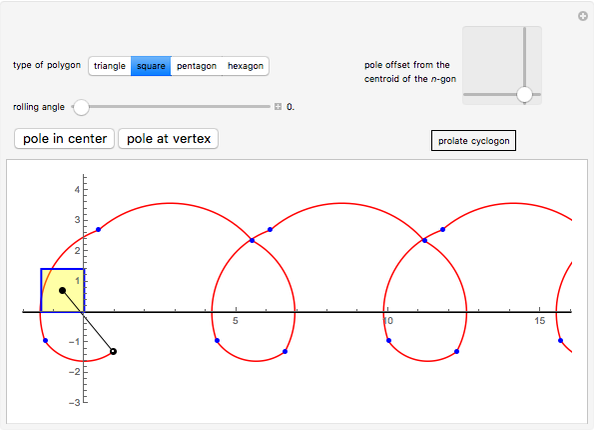
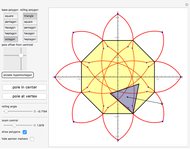
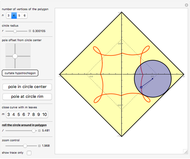
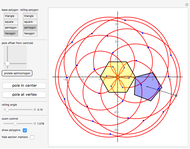
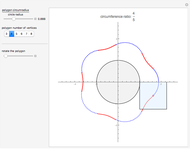
This Demonstration traces the path of a point attached to a regular polygon rolling without slipping along a straight line. The point is called the pole or tracing point.

[more]

If the pole is a vertex of the polygon (Snapshot 1), the traced curve is called a cyclogon.

If the pole is inside the polygon, the curve is a curtate cyclogon (Snapshot 3). If outside the polygon, it is a prolate cyclogon (Snapshot 4).

[less]

Contributed by: Erik Mahieu (March 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The rolling polygon and the pole are subject to a sequence of three geometric transformations:

1. A stepwise rotation by a multiple of around the centroid of the polygon.

2. A stepwise translation along the axis by an edge length: .

3. A continuous rotation by 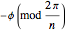around a point on the axis where it was moved by the previous translation.

The variable is the angular position of the polygon around its centroid.

The variable is the number of vertices of the polygon.

The resulting cyclogon is a sequence of circular arcs with the same subtending angle: . The centers of the arcs are on the axis and are each an edge length apart.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send