Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Tracing Card Paths during Perfect Shuffles

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

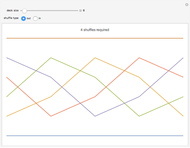
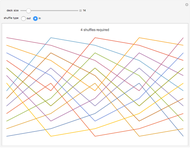
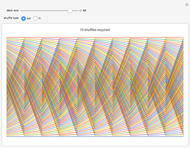
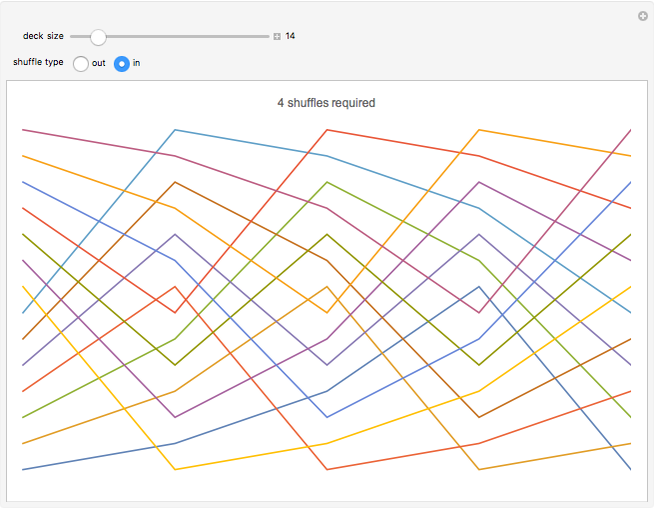
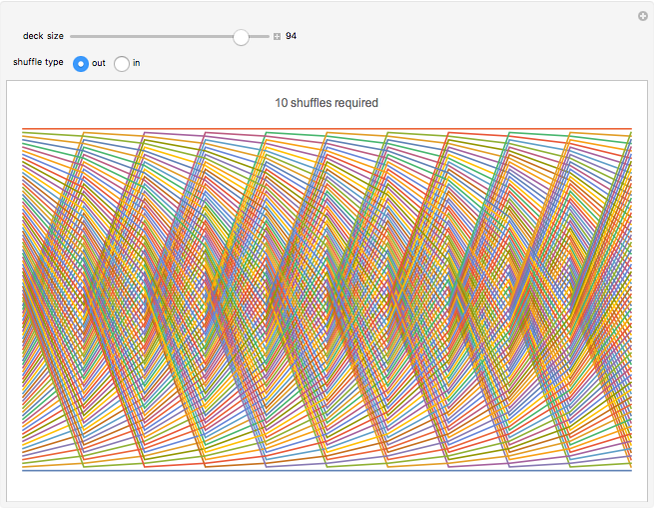
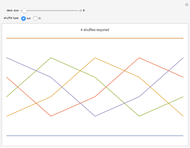
This Demonstration displays the path that each card takes through a deck over the course of a sequence of consecutive perfect shuffles. Each colored line traces the path of one card as a plot of position versus time. Use the controls to adjust the number of cards in the deck and whether the shuffle is an in-shuffle or an out-shuffle. The minimum number of shuffles required to return the deck to its original order is shown at the top.

Contributed by: Adam Rumpf (November 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

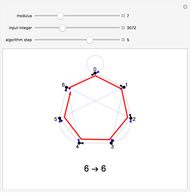
A perfect shuffle is a type of riffle shuffle wherein a deck of cards is divided into two equal halves, and then the halves are interlaced with one another. There are two types of perfect shuffles: an out-shuffle, for which the original top card remains on top, and an in-shuffle, for which the original top card becomes the new second card [1].

Repeating a perfect shuffle on a finite deck must eventually return it to its original order. If the deck contains cards (where is even), then the number of out-shuffles required is the multiplicative order of modulo , while the number of in-shuffles required is the multiplicative order of modulo [2].

References

[1] P. Diaconis, R. L. Graham and W. M. Kantor, "The Mathematics of Perfect Shuffles," Advances in Applied Mathematics, 4(2), 1983 pp. 175–196. doi:10.1016/0196-8858(83)90009-X.

[2] N. J. A. Sloane. The On-Line Encyclopedia of Integer Sequences. "Multiplicative Order of 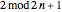." oeis.org/A002326.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send