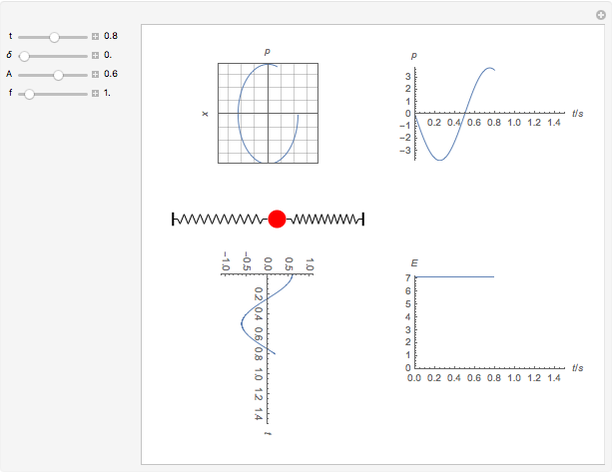
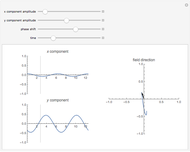
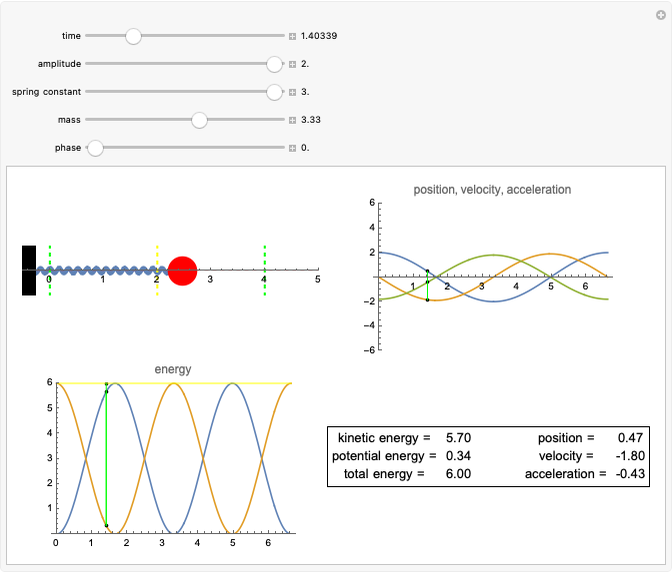
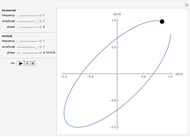
Trajectory of a Harmonic Oscillator in Phase Space
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
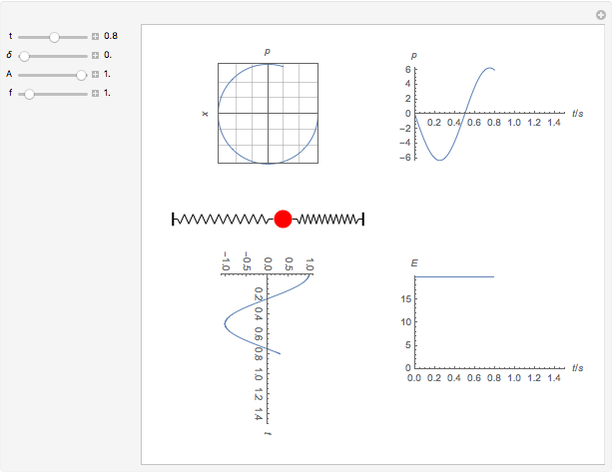
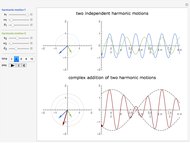
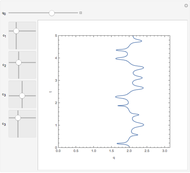
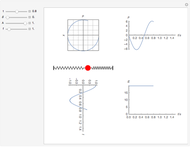
You can observe how the trajectory of a harmonic oscillator in phase space evolves in time and how it depends on the characteristic values of the oscillator: the amplitude 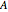 , the frequency
, the frequency 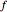 , and the damping constant
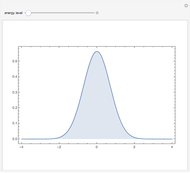
, and the damping constant  . In addition, the energy
. In addition, the energy 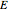 as a function of time
as a function of time  is shown.
is shown.
Contributed by: Hans-Joachim Domke (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation