Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Transformations of Complex, Dual, and Hyperbolic Numbers

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

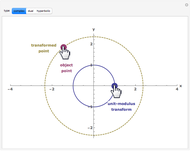
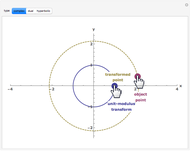
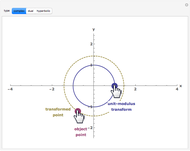
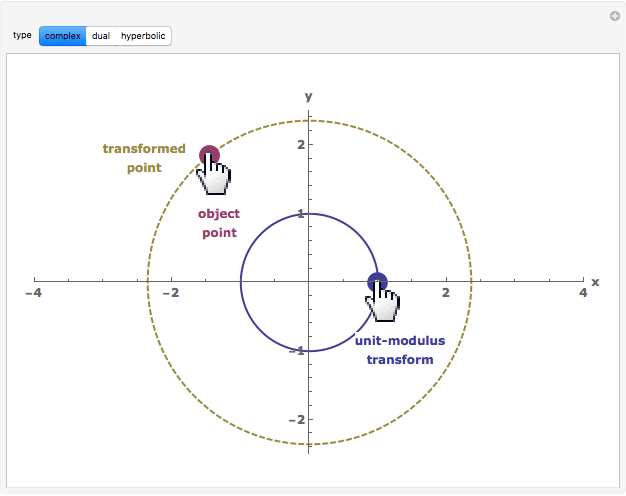
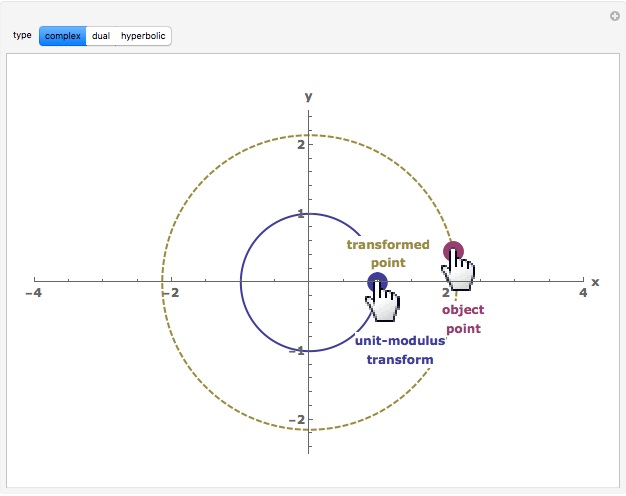
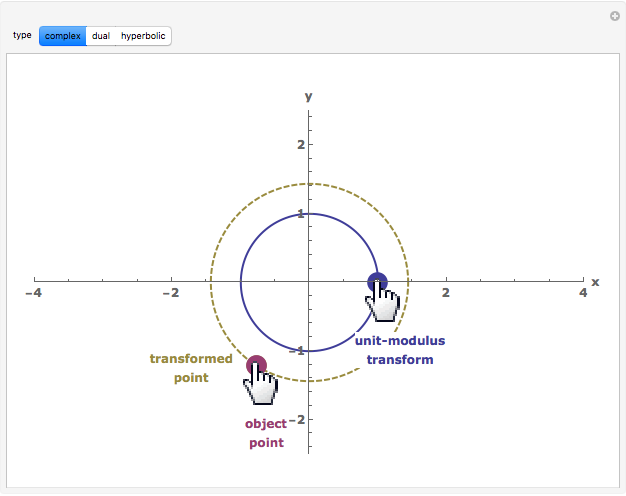
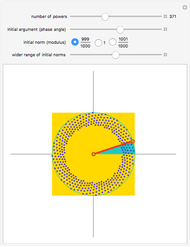
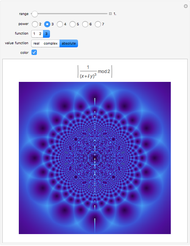
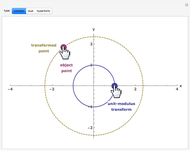
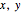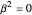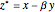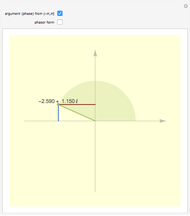
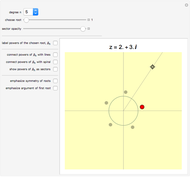
This Demonstration compares the multiplicative transformation properties on the plane of complex, dual, and hyperbolic numbers. These number types share the form , where and are real numbers and has the defining characteristics: for complex numbers, for dual numbers, and for hyperbolic numbers. Their conjugates share the form and their modulus the form 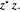The figure shows, for the selected number type,

[more]

1. a transform point on its unit-modulus locus (in blue),

2. an object point in the plane (in red), and

3. the point resulting from their multiplicative transform on its trajectory (in brown).

In the complex plane, multiplying by a unit-modulus transform produces a rotation about the origin; in the dual plane, it produces a translation in the pure dual direction, and in the hyperbolic plane, a traversal of an hyperbola that passes through the object point.

[less]

Contributed by: Fred Klingener (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Hyperbolic numbers (sometimes called split-complex numbers) are useful for measuring distances in the Lorentz space-time plane (see G. Sobczyk, "The Hyperbolic Number Plane," The College Mathematics Journal, 26(4), 1995 pp. 268–280).

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send