Transformations on Graphs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
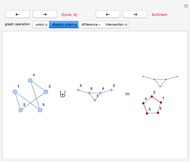
The line graph  of a simple graph
of a simple graph 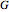 is the graph obtained by taking the edges of
is the graph obtained by taking the edges of 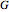 as vertices, and joining two of these vertices whenever the corresponding edges of
as vertices, and joining two of these vertices whenever the corresponding edges of 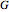 have a vertex in common. Given
have a vertex in common. Given  , it might be impossible to find
, it might be impossible to find 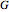 ; for instance, if
; for instance, if 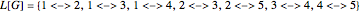 . The complement of a simple graph
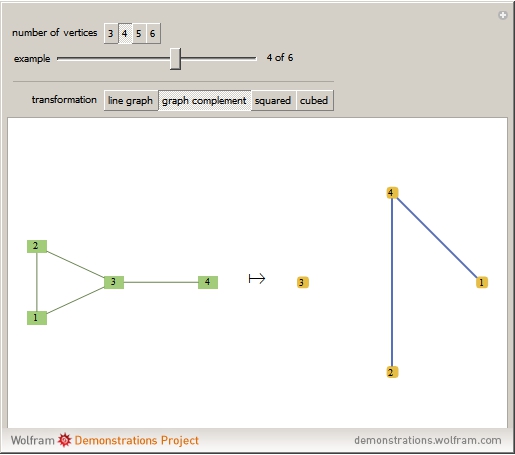
. The complement of a simple graph 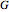 is obtained by taking the vertices of
is obtained by taking the vertices of 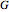 and joining two of them whenever they are not joined in
and joining two of them whenever they are not joined in 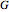 . Complements of complete graphs are always empty graphs (without edges) and vice versa. The square, cube, or in general, the
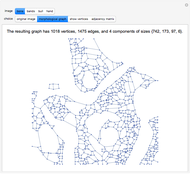
. Complements of complete graphs are always empty graphs (without edges) and vice versa. The square, cube, or in general, the 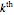 power of a graph
power of a graph 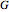 is obtained by taking the vertices of
is obtained by taking the vertices of 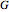 and joining them if there is a path of length at most
and joining them if there is a path of length at most  joining them. The powers of complete graphs are isomorphic to themselves. Can you find a graph such that its square is different from its cube? Can you find a graph such that its cube is not complete?
joining them. The powers of complete graphs are isomorphic to themselves. Can you find a graph such that its square is different from its cube? Can you find a graph such that its cube is not complete?
Contributed by: Jaime Rangel-Mondragon (August 2011)
Based on work by: Roger Germundsson, Charles Pooh, Jae Bum Jung, Yan Zhuang, Henrik Tidefelt, and Tim Shedelbower
Open content licensed under CC BY-NC-SA
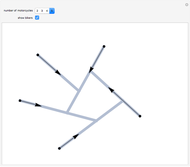
Snapshots
Details
Permanent Citation