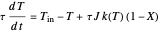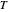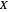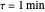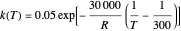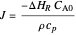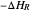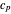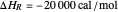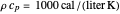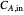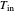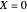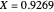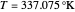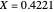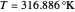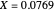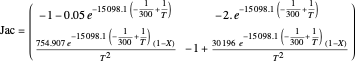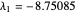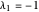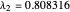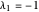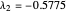,
,
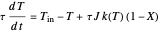 ,
,
where 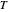 and
and 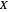 are the reactor's temperature and conversion fraction,
are the reactor's temperature and conversion fraction, 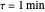 is the reactor's residence time,
is the reactor's residence time, 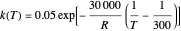 is the rate constant,
is the rate constant, 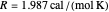 ,
, 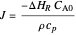 , where
, where 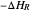 is the heat of reaction,
is the heat of reaction, 
 is the fluid density, and
is the fluid density, and 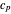 is the fluid heat capacity. It is assumed that
is the fluid heat capacity. It is assumed that 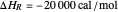 and
and 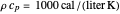 .
.
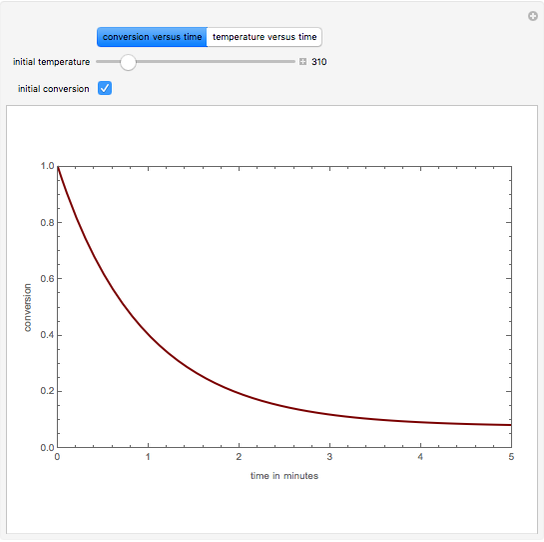
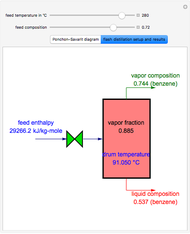
The reactor's feed has a concentration, 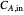 , and a temperature,
, and a temperature, 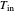 , chosen equal to 2 moles/liter and 300 Kelvin. The reactor's initial temperature is set by the user. The reactor is initially filled with either pure solvent (i.e.,
, chosen equal to 2 moles/liter and 300 Kelvin. The reactor's initial temperature is set by the user. The reactor is initially filled with either pure solvent (i.e.,  ) or with pure feed (i.e.,
) or with pure feed (i.e., 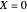 ). Three steady states are found if one solves the nonlinear system of equations, which is obtained by setting the left-hand side of the governing equations equal to zero. These steady states are the following:
). Three steady states are found if one solves the nonlinear system of equations, which is obtained by setting the left-hand side of the governing equations equal to zero. These steady states are the following:
SS1: high conversion with 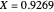 and
and 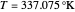
SS2: intermediate conversion with 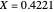 and
and 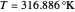
SS3: low conversion with 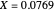 and
and 
A stability analysis reveals that only the first and last steady states are stable (i.e., SS1 and SS3). Indeed, the Jacobian matrix is the following:
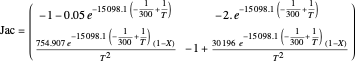
Eigenvalues for the three steady states can be computed and are equal to:
1/ for SS1: 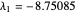 and
and  (both are negative)
(both are negative)
2/ for SS2: 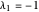 and
and 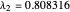 (eigenvalues have opposite signs)
(eigenvalues have opposite signs)
3/ for SS3: 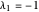 and
and 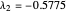 (both are negative)
(both are negative)
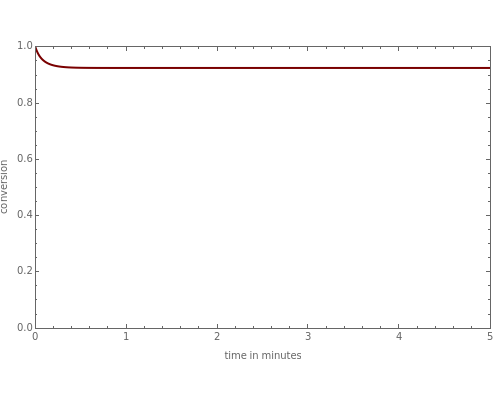
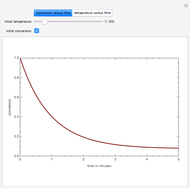
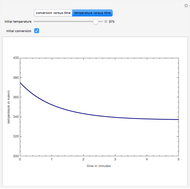
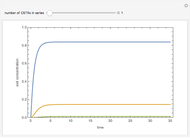
This Demonstration plots the transient behavior of the reactor's concentration and temperature. It is clear from the snapshots that only SS1 and SS3 can be reached depending on the initial condition. One snapshot shows that for certain initial conditions the trajectory approaches SS2, then goes to SS1. Indeed, SS2 is a saddle point. One can conclude that adiabatic CSTR reactors show very interesting behavior such as steady state multiplicity.
[less]

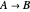 , taking place in an adiabatic CSTR (continuous stirred-tank reactor). The relevant equations derived from the mass and energy balances are the following:
, taking place in an adiabatic CSTR (continuous stirred-tank reactor). The relevant equations derived from the mass and energy balances are the following: