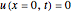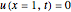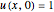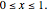Transient Heat Conduction Using Chebyshev Collocation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
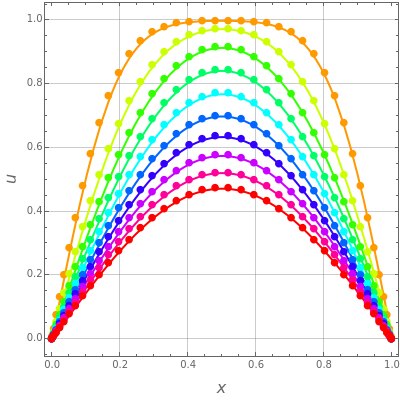
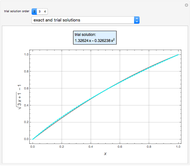
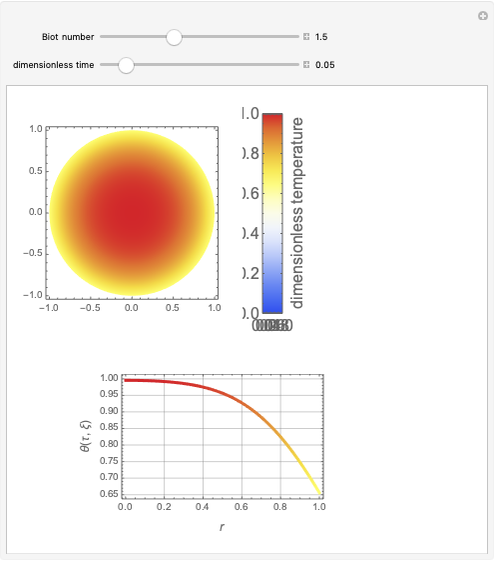
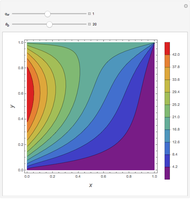
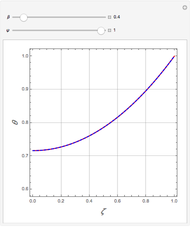
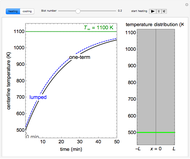
Consider the one-dimensional heat equation given by
[more]
Contributed by: Housam Binous, Brian G. Higgins, and Ahmed Bellagi (April 2013)
Open content licensed under CC BY-NC-SA
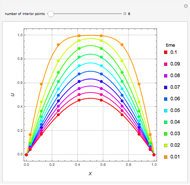
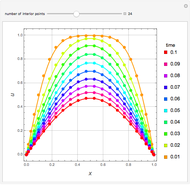
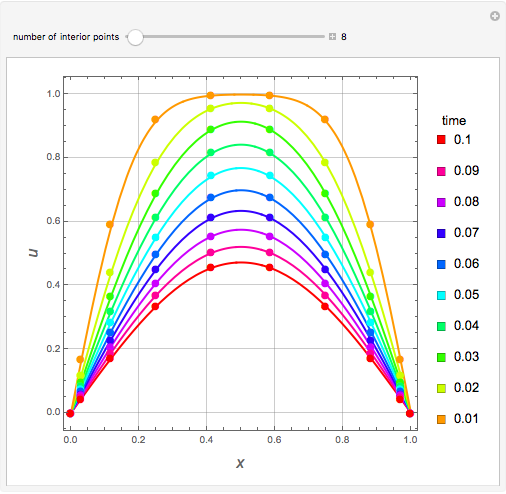
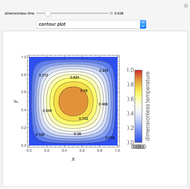
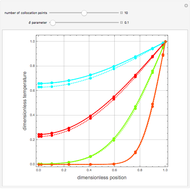
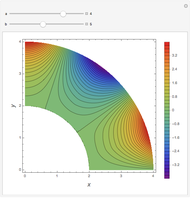
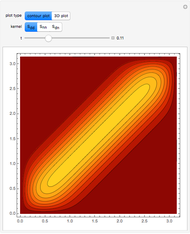
Snapshots
Details
In the discrete Chebyshev–Gauss–Lobatto case, the interior points are given by 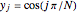 . These points are the extremums of the Chebyshev polynomial of the first kind
. These points are the extremums of the Chebyshev polynomial of the first kind 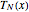 .
.
The  Chebyshev derivative matrix at the quadrature points,
Chebyshev derivative matrix at the quadrature points,  , is an
, is an  matrix given by
matrix given by
 ,
,  ,
, 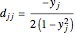 for
for  , and
, and  for
for 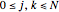 and
and 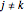 ,
,
where  for
for 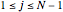 and
and  .
.
The second-order partial spacial derivatives are obtained using 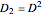 .
.
An affine transformation, 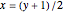 , allows shifting from interval
, allows shifting from interval 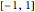 to
to 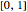 .
.
Reference
[1] L. N. Trefethen, Spectral Methods in MATLAB, Philadelphia: SIAM, 2000.
Permanent Citation