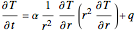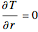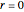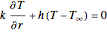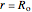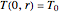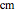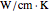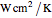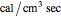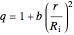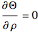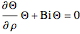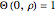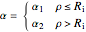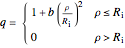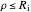Transient Heat Conduction with a Nuclear Heat Source

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
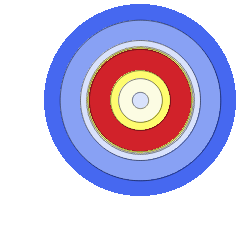
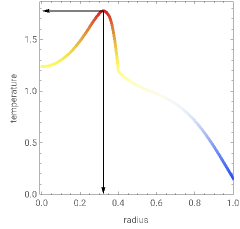
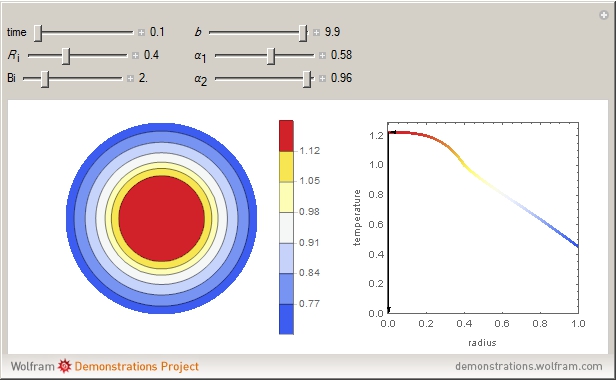
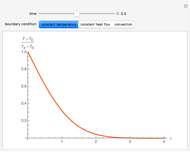
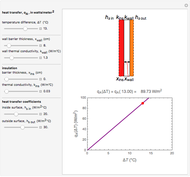
Consider a spherical nuclear fuel element consisting of a sphere of fissionable material of radius 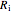 , surrounded by a spherical shell of alloy cladding with outer radius
, surrounded by a spherical shell of alloy cladding with outer radius 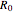 , initially at temperature
, initially at temperature 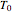 , that is suddenly immersed at
, that is suddenly immersed at  in a cooling bath of temperature
in a cooling bath of temperature 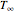 . The heat equation describing this system is:
. The heat equation describing this system is:
Contributed by: Clay Gruesbeck (January 2017)
Open content licensed under CC BY-NC-SA
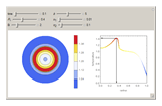
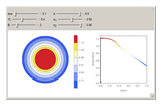
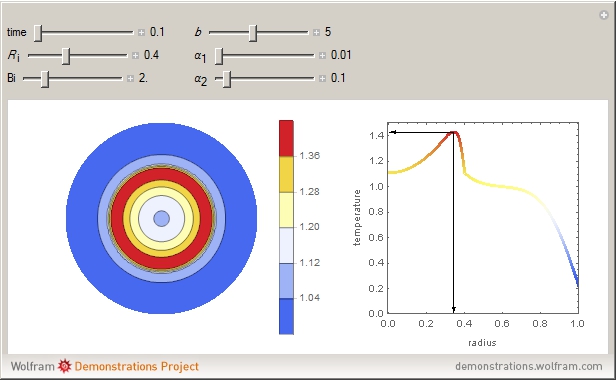
Snapshots
Details
A similar steady-state problem is solved in [1].
Reference
[1] R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport Phenomena, rev. 2nd ed., New York: John Wiley & Sons, Inc., 2007.
Permanent Citation