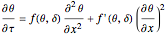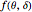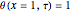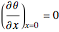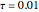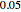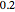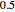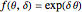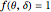Transient Heat Conduction with Temperature-Dependent Thermal Conductivity
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
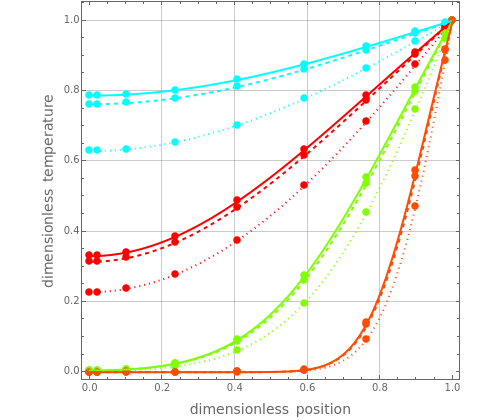
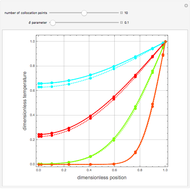
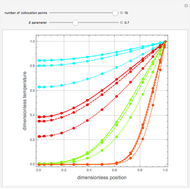
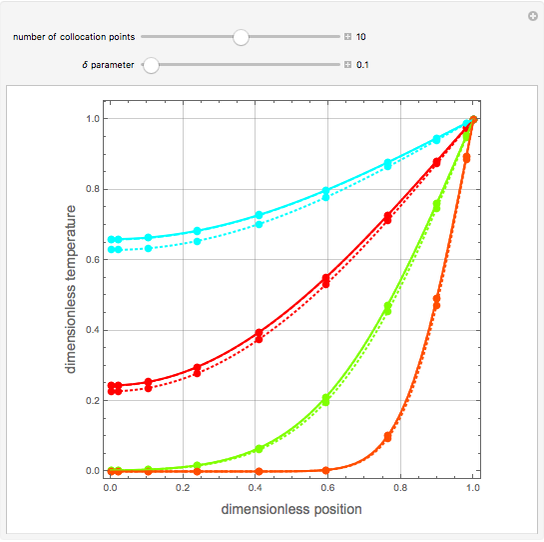
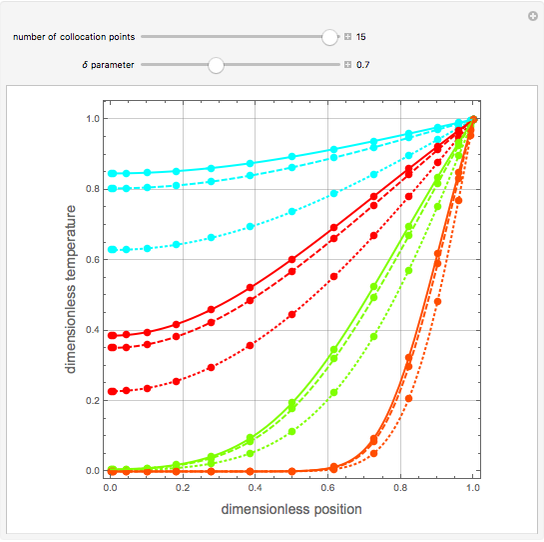
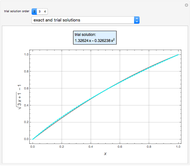
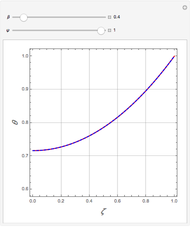
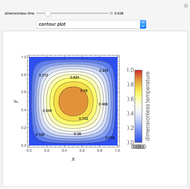
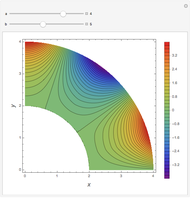
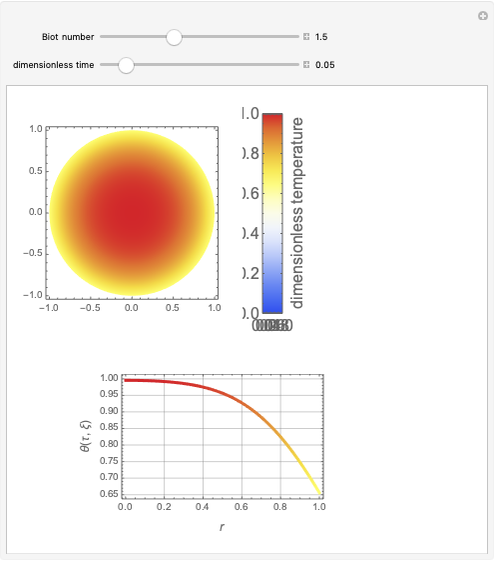
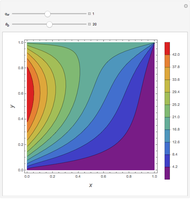
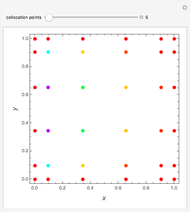
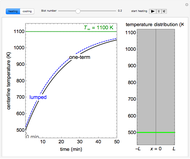
Consider transient heat conduction in a finite slab with temperature-dependent thermal conductivity. The phenomenon is governed by the following dimensionless equation:
[more]
Contributed by: Housam Binous and Brian G. Higgins (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] S. H. Lin, "Transient Heat Conduction with Temperature-Dependent Thermal Conductivity by the Orthogonal Collocation Method," Letters in Heat and Mass Transfer, 5(1), 1978 pp. 29–39.
Permanent Citation