Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Transient Response of a Semiconductor Laser

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

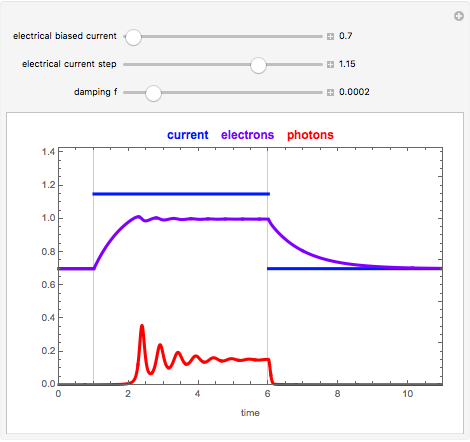
The transient response of a semiconductor laser is calculated by solving the coupled rate equations, which are two differential equations involving the electron and the photon densities. The normalized electrical current 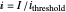injected into the laser suddenly increases from to 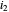; the electron and photon normalized densities are shown (in purple and red). Time is normalized by the lifetime of the electron. Photons are created by electron-hole recombination in the laser. The interaction between electrons and photons, described by the coupled rate equations, leads to damped relaxation oscillations. The normalized time required to reach photon and electron density equilibrium values is around 1-3, and the actual time a few nanoseconds, since the typical value of the lifetime of the electron is around 1 nanosecond.

[more]

Therefore, current modulated semiconductor lasers can be used to emit optical digital signals in lightwave communication systems up to a few gigabit/second. For simplicity, the coupled rate equations used have been derived with reasonable approximations and the qualitative predictions can be trusted and are verified by experiments.

A semiconductor LASER (Light Amplification by Stimulated Emission of Radiation) is a very compact light source (0.2 mm long) in which electric current (a few mA) is converted into coherent optical power with high efficiency. In 1970, the successful Continuous Wave (CW) operation of the Double-Heterostructure laser at room temperature coincided with the achievement of low loss (1 dB/km) optical fiber. These high improvements of both laser and optical fiber created strong excitement worldwide.

[less]

Contributed by: Philippe Brosson (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

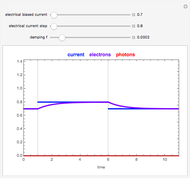
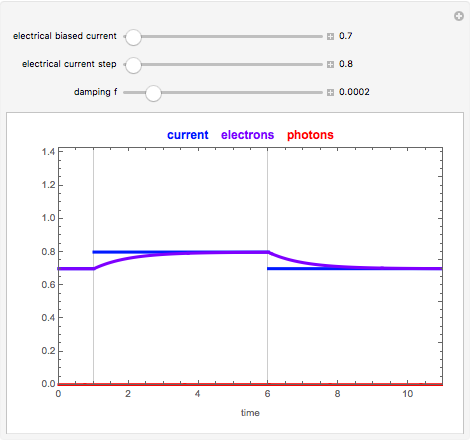
Snapshot 1: Transient response of the laser for 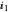= 0.7 and 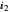=0.8 (below the threshold current =1). The photon density is very low (spontaneous emission) and the carrier density builds up to a value lower than threshold carrier density =1.

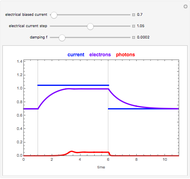
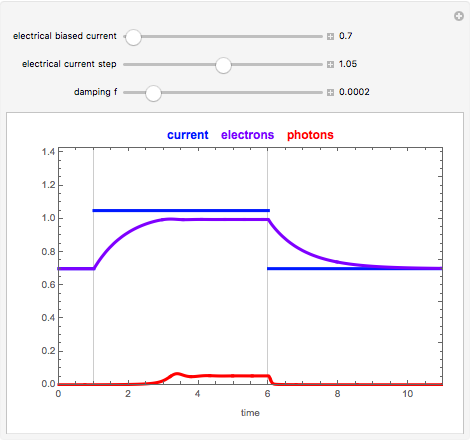
Snapshot 2: Transient response of the laser for 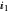=0.7 and 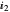=1.05 (slightly above threshold). The photon density is higher compared to Snapshot 1 and the carrier density builds up towards 1.

Snapshot 3: Transient response of the laser for 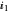=0.7 and 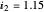(above threshold) . The photon density increases sharply when the carrier density reaches threshold. The time delay between the rising edge of the current step and the stimulated emission is around 1. Relaxation oscillations are due to interaction between electrons and photons. An increase of the photon density induces a reduction of the carrier density which in turn causes a decrease of the optical gain, resulting in a reduction of the photon density.

Snapshot 4: Transient response of the laser for 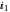=0.98 and 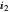=1.15. The carrier density reaches threshold earlier, compared to Snapshot 3, resulting in an almost zero time delay between the rising edge of the current step and the stimulated emission.

Snapshot 5: Transient response of the laser in the case of low damping (0.0002) of the relaxation oscillations. The relaxation oscillations frequency is roughly proportional to 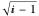; 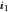=0.8 and 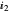=1.3.

Snapshot 6: Transient response of the laser in the case of strong damping (0.001) of the relaxation oscillations; 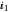=0.8 and 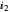=1.3.

H. Kressel and J. K. Butler, Semiconductor Lasers and Heterojunction LEDs, Academic Press, 1977.

H. C. Casey, Jr. and M. B. Panish, Heterostructure Lasers, Academic Press, 1978.

G. H. B. Thomson, Physics of Semiconductor Laser Devices, John Wiley, 1980.

G. P. Agrawal and N. K. Dutta, Semiconductor Lasers, 2nd ed., Van Nostrand Reinhold, 1993.

P. Brosson, Semiconductor Lasers and Integrated Devices.

See Semiconductor Lasers operating principle (PDF) and High Speed Lasers (PDF) on the author's website for more information.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send