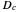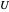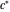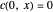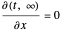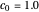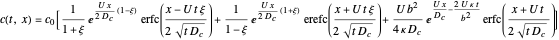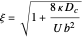Transport and Deposition of Colloid in Rock Fractures
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
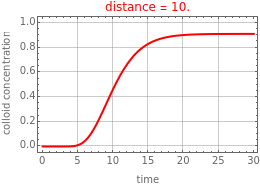
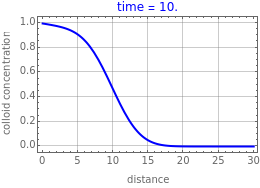
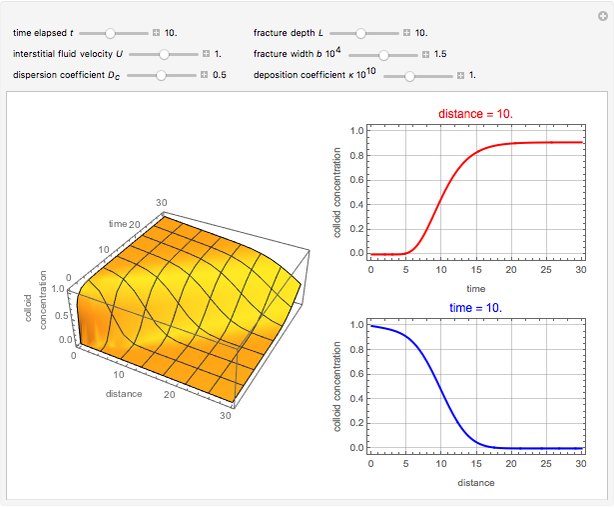
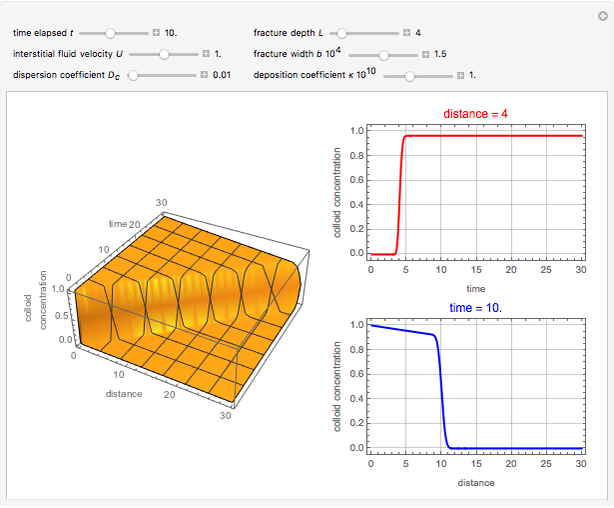
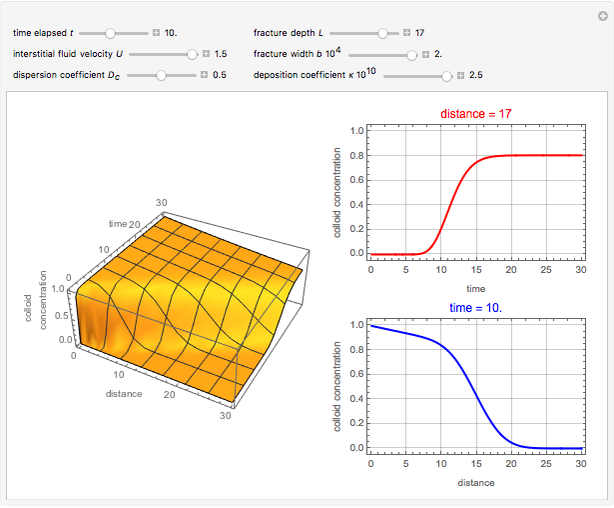
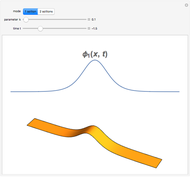
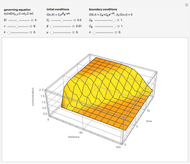
This Demonstration illustrates the dynamics of transport and deposition of colloidal particles in the walls of a rock fracture. The partial differential equation governing colloid transport in a one-dimensional fracture idealized as two parallel plates can be written as [1]:
[more]
Contributed by: Clay Gruesbeck (July 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
Permanent Citation