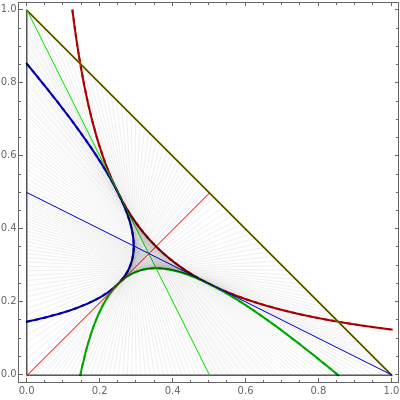
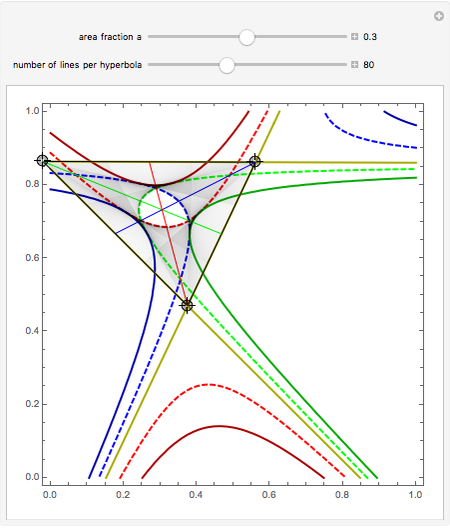
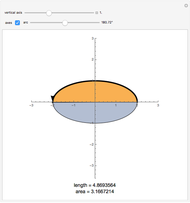
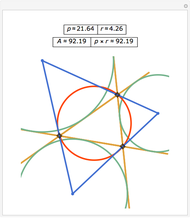
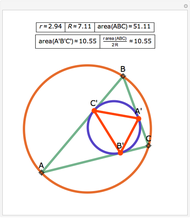
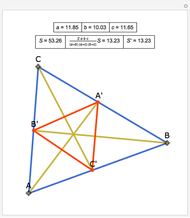
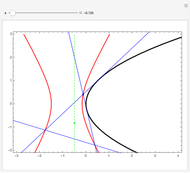
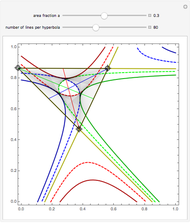
Area bisectors are straight lines that divide a triangle into two parts of equal area. They are all tangent lines to three different hyperbolas whose asymptotes are the straight lines containing the sides of the triangle. This Demonstration shows the bisectors and the hyperbolas for any triangle. For any fraction of the total area , there are two lines emanating from each vertex that divide the triangle into a part with of the total area and a part with of the total area. These six lines are tangent to six hyperbolas, and this scenario can be viewed by controlling the value of with the top slider.