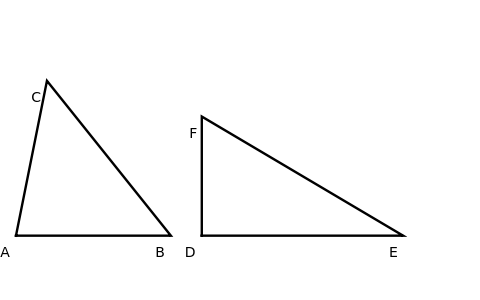
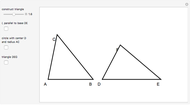
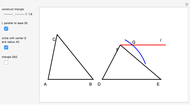
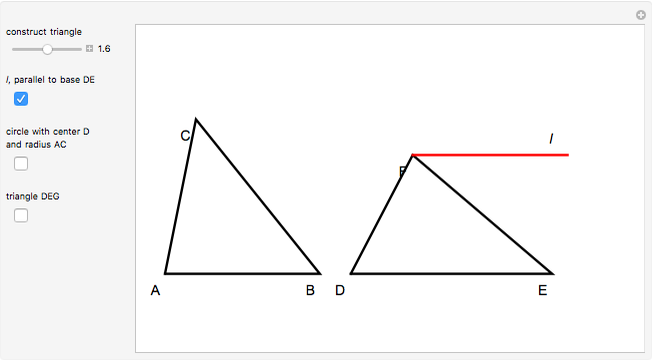
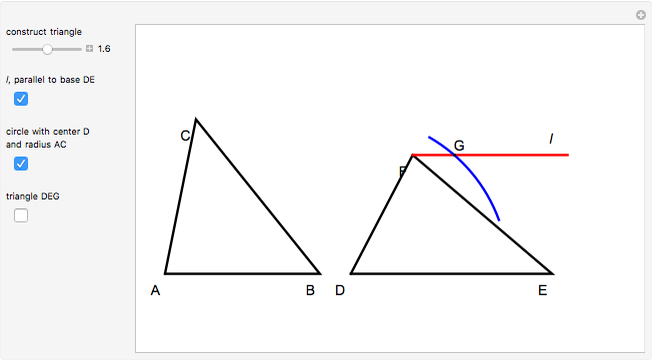
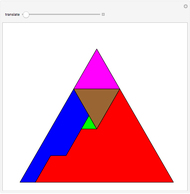
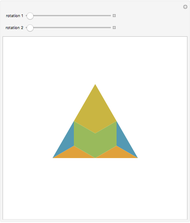
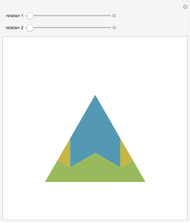
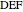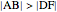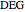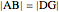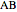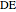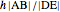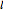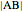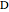Triangles with Equal Area Are Equidecomposable (Equivalent by Dissection)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
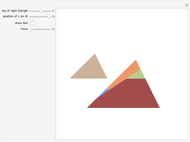
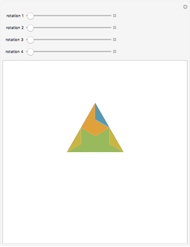
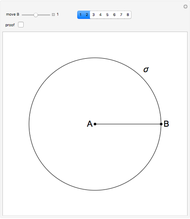
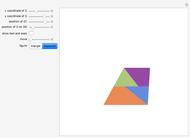
A dissection of a polygon 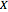 is a set of polygons that cover
is a set of polygons that cover 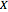 exactly without gaps or overlaps. Two polygons are equidecomposable (or equivalent by dissection) if there is a dissection of one that can be reassembled to form the other. In 2D, two polygons of equal area are equidecomposable. On the other hand in 3D, even the cube and the tetrahedron of equal volume are not equidecomposable.
exactly without gaps or overlaps. Two polygons are equidecomposable (or equivalent by dissection) if there is a dissection of one that can be reassembled to form the other. In 2D, two polygons of equal area are equidecomposable. On the other hand in 3D, even the cube and the tetrahedron of equal volume are not equidecomposable.
Contributed by: Izidor Hafner (May 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] B. I. Agrunov and M. B. Balk, Elemenarnaja Geometrija (in Russian), (Elementary Geometry), Moscow 1966, pp. 174–175.
Permanent Citation