Trilateration and the Intersection of Three Spheres

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Trilateration is used in technologies such as GPS to find the exact location of a point on Earth or in space. It determines a location by means of three distances to known points in space, such as orbiting satellites.
[more]
Contributed by: Erik Mahieu (December 2015)
Open content licensed under CC BY-NC-SA
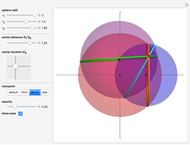
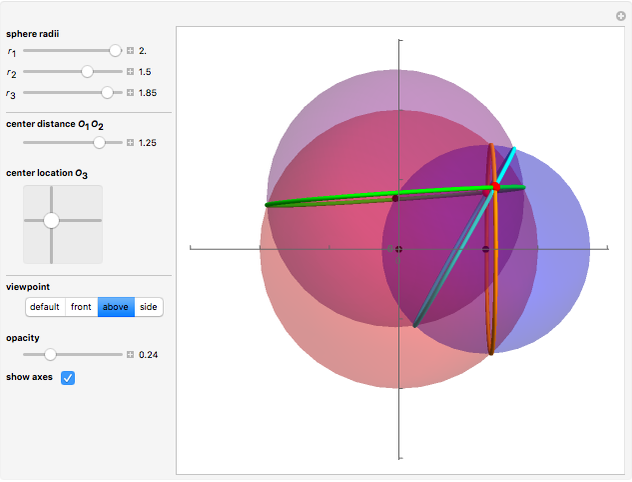
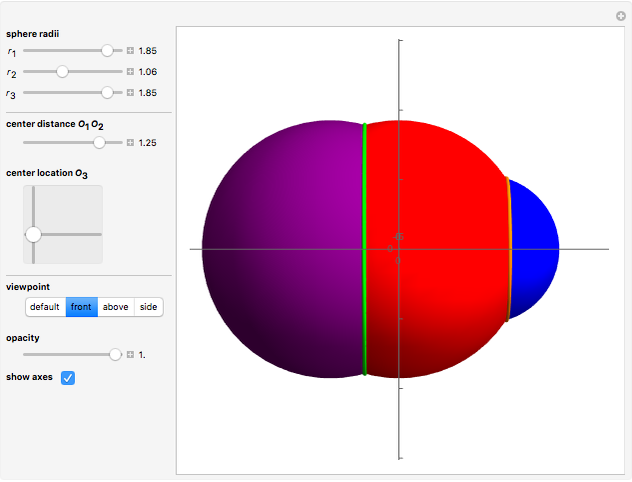
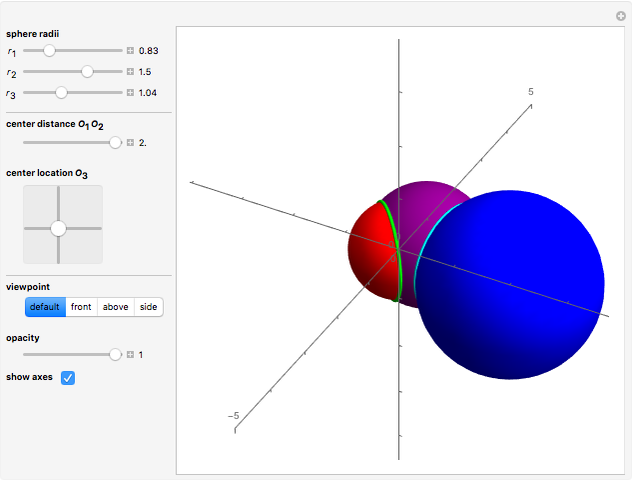
Snapshots
Details
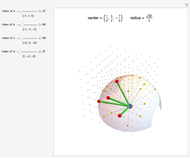
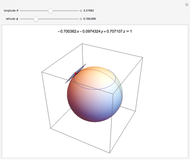
All three centers of the spheres are in the plane  :
: 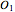 at
at 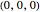 ,
,  at
at 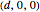 ,
, 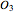 at
at  .
.
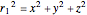 ,
,
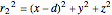 ,
,
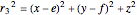 .
.
The two intersection points are found by solving these three equations for  ,
, 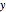 , and
, and  .
.
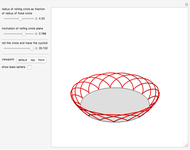
The intersection circles have the parametric form of a circle on a sphere, centered at the origin and with the  axis as its normal, rotated by an angle
axis as its normal, rotated by an angle  around the
around the 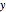 axis and
axis and 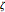 around the
around the  axis:
axis:
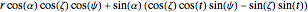 ,
,
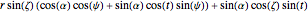 ,
,
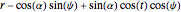 ,
,
where
 is the angular radius of the circle,
is the angular radius of the circle,
 is the rotation around the
is the rotation around the 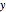 axis,
axis, 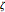 is the rotation around the
is the rotation around the  axis,
axis,
and  is a parameter running around the circle, from 0 to
is a parameter running around the circle, from 0 to 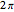 .
.
Permanent Citation