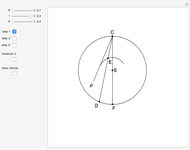
Trisecting an Angle Using the Cycloid of Ceva
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
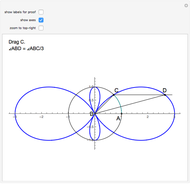
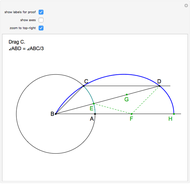
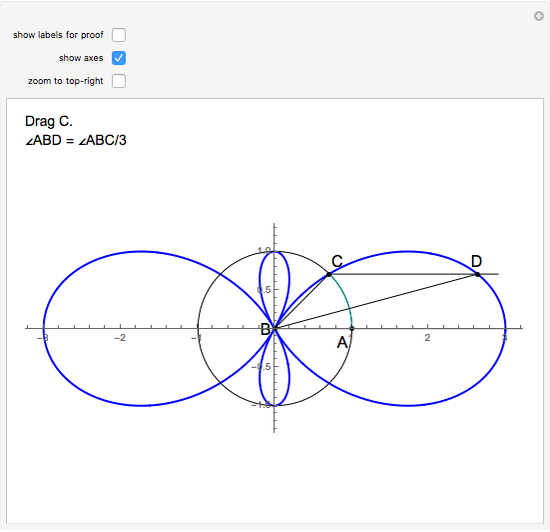
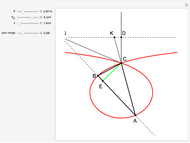
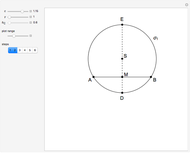
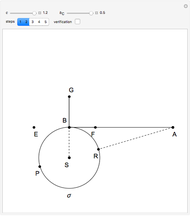
The cycloid of Ceva has the polar equation  . To trisect the angle
. To trisect the angle  , construct a line parallel to the polar axis (the positive
, construct a line parallel to the polar axis (the positive  axis). Let
axis). Let 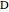 be the point of intersection of the cycloid and the line. Then the angle
be the point of intersection of the cycloid and the line. Then the angle 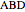 is one-third of the angle
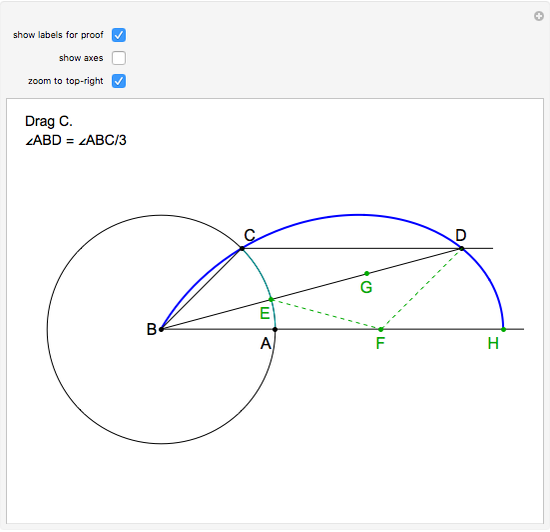
is one-third of the angle  . Proof: let angle
. Proof: let angle 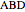 be
be  and let the point
and let the point 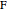 on the
on the  axis be such that
axis be such that 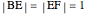 . Let
. Let  be the orthogonal projection of
be the orthogonal projection of 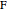 on the line
on the line 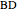 . The angle
. The angle 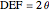 , so
, so  . Since
. Since 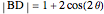 ,
,  ,
, 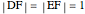 . So angle
. So angle 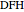 equals
equals 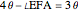 , but
, but 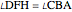 .
.
Contributed by: Izidor Hafner (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation