Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Twenty Tetrahedra in Icosahedral Cluster

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

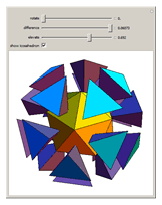
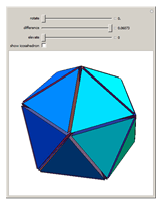
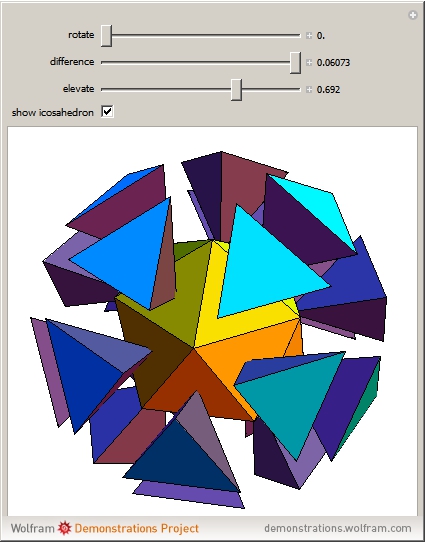
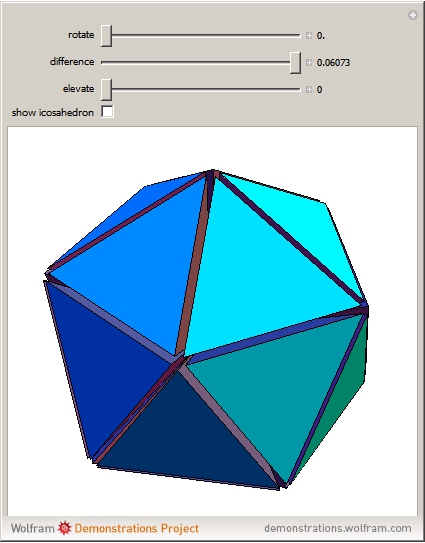
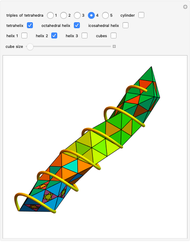
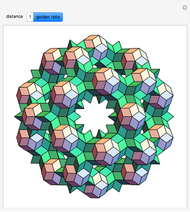
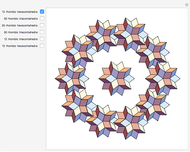
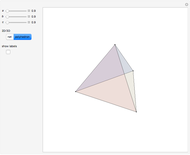
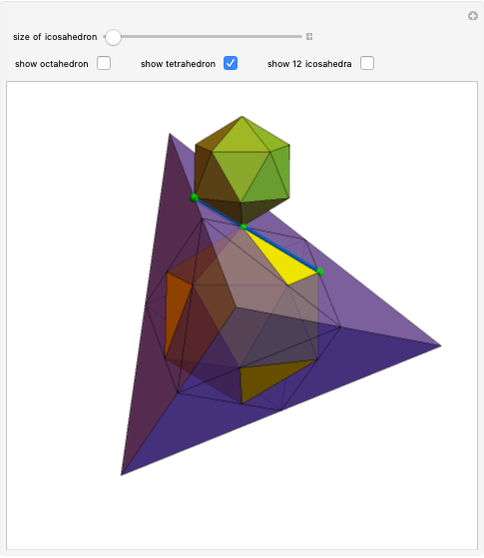
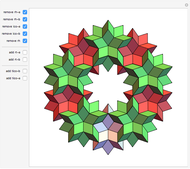
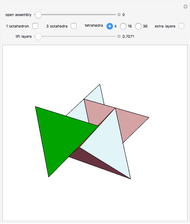
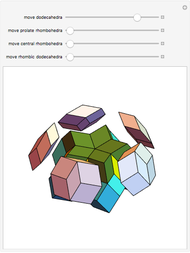
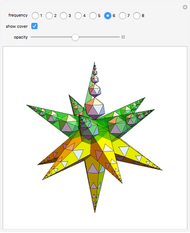
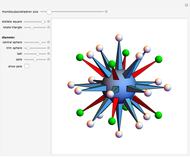
A golden tetrahedron is the tetrahedral part of a golden rhombohedron. Twenty such golden tetrahedra can be put together to form a regular icosahedron. (If regular tetrahedra are used, there are gaps.) Twenty regular tetrahedra can be brought to meet face to face by rotating around the axes through the centers of the tetrahedra and the icosahedron.

Contributed by: Sándor Kabai (July 2014)
Using information received from: Klee Irwin and Fang Fang
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] F. Fang, K. Irwin, J. Kovacs, and G. Sadler. "Cabinet of Curiosities: The Interesting Geometry of the Angle β = arccos((3ϕ - 1)/4)." arxiv.org/abs/1304.1771.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send