Two-Dimensional Oscillator in Magnetic Field

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
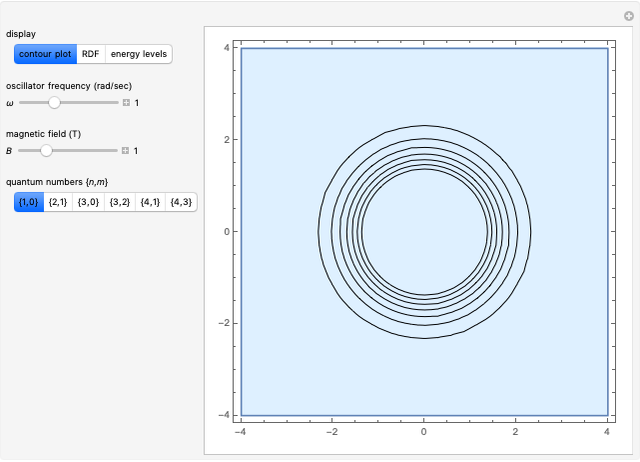
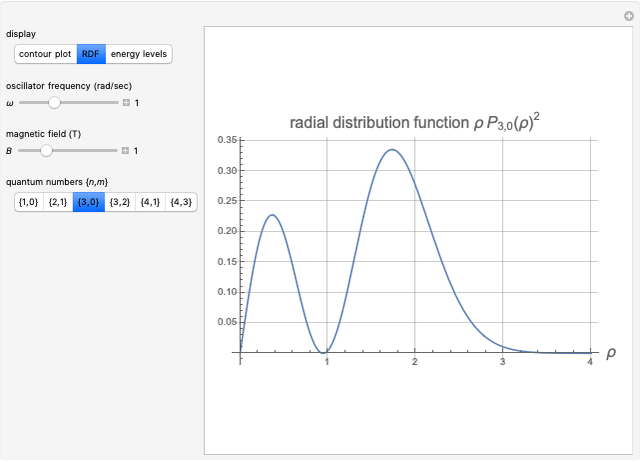
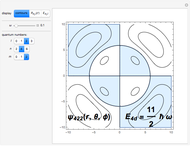
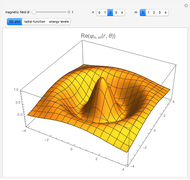
The two-dimensional problem of a charged isotropic harmonic oscillator in a constant magnetic field can be solved exactly, as worked out in the Details. You can choose to display: (1) a contour plot of the solutions; (2) the radial distribution function in cylindrical coordinates; or (3) an energy-level diagram. You can select the oscillator frequency 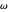 , the magnetic field
, the magnetic field 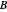 and the quantum numbers
and the quantum numbers 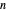 and
and 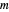 . In the contour plots, positive and negative regions are colored blue and yellow, respectively.
. In the contour plots, positive and negative regions are colored blue and yellow, respectively.
Contributed by: S. M. Blinder (March 2019)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For a charged particle (charge  , mass
, mass  ) in a magnetic field, the canonical form for the nonrelativistic Hamiltonian is given by
) in a magnetic field, the canonical form for the nonrelativistic Hamiltonian is given by
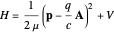 ,
,
where 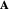 is the vector potential. The magnetic field is given by
is the vector potential. The magnetic field is given by 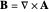 . We consider an electron (
. We consider an electron (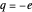 ) confined to the
) confined to the 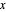 -
-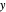 plane, bound by an isotropic harmonic-oscillator potential and subjected to a constant magnetic field
plane, bound by an isotropic harmonic-oscillator potential and subjected to a constant magnetic field  in the
in the  direction. This field can be represented by the vector potential
direction. This field can be represented by the vector potential 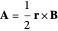 , such that
, such that
 ,
,
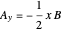 ,
,
 .
.
The Schrödinger equation, in Cartesian coordinates, can then be written
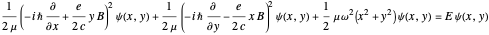 .
.
Expanding the squares, we obtain
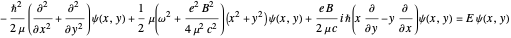 .
.
Note now that 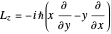 , the
, the  component of angular momentum, and that
component of angular momentum, and that 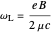 , the Larmor frequency for an electron. It is convenient now to transform to cylindrical coordinates (
, the Larmor frequency for an electron. It is convenient now to transform to cylindrical coordinates (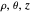 ), such that
), such that 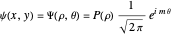 , which is an eigenfunction of
, which is an eigenfunction of 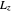 with eigenvalues
with eigenvalues 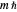 ,
, 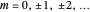 . The radial function
. The radial function 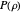 satisfies the equation
satisfies the equation
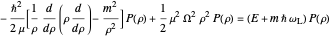 ,
,
where  . This has the form of the unperturbed two-dimensional oscillator and has the solutions (unnormalized, using atomic units
. This has the form of the unperturbed two-dimensional oscillator and has the solutions (unnormalized, using atomic units  ):
):
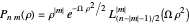 ,
, 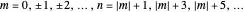 ,
,
where 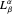 is an associated Laguerre polynomial. The corresponding energies are
is an associated Laguerre polynomial. The corresponding energies are
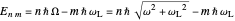 .
.
Using atomic units and expressing 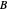 in teslas (T),
in teslas (T), 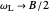 . The energy, expanded in powers of the magnetic field, is then given by
. The energy, expanded in powers of the magnetic field, is then given by
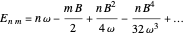 .
.
Permanent Citation