Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Two Models of Projective Geometry

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

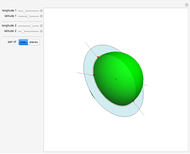
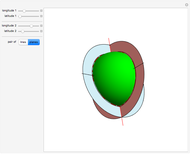
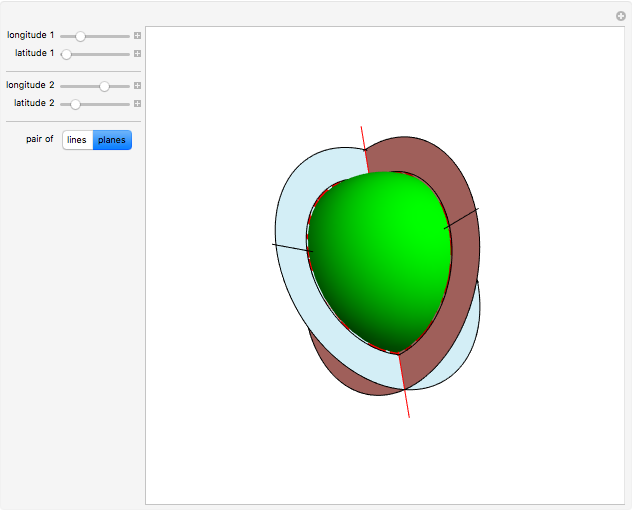
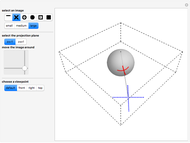
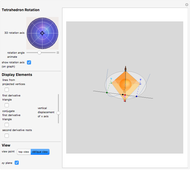
In the first model of 2D elliptic geometry, "points" and "lines" are the lines and planes through the origin in 3D, respectively. These axioms are satisfied: two "points" determine a "line" (because the two ordinary lines determine an ordinary plane), and two "lines" determine a "point" (intersect the two ordinary planes to get an ordinary line). There are no parallel "lines", because all ordinary planes intersect.

[more]

Another definition uses the points and great circles on a sphere with opposite points identified. This definition seems more natural than the first because the points are more point-like and the lines are one-dimensional, but the identification of opposite points is somewhat disorienting, especially for the great circles.

The two models are clearly related: a line through the center of a sphere intersects the sphere in two opposite points and a plane through the center intersects the sphere in a great circle.

For the choice of a pair of planes, the sliders govern the planes' normals.

[less]

Contributed by: George Beck (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

detailSectionParagraph
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send