Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Unbiased and Biased Estimators

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

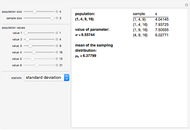
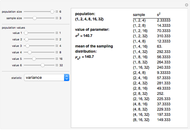
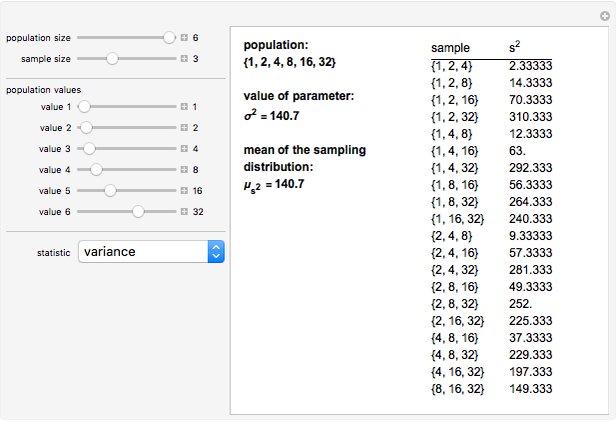
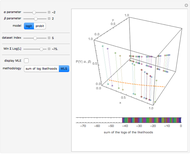
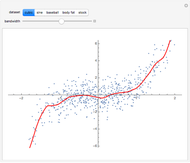
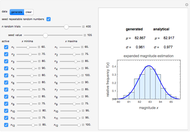
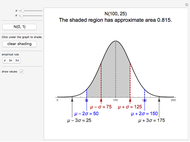
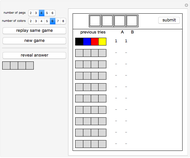
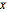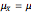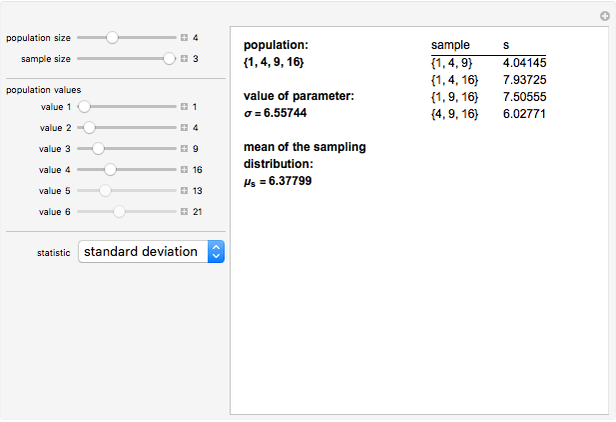
A statistic is called an unbiased estimator of a population parameter if the mean of the sampling distribution of the statistic is equal to the value of the parameter. For example, the sample mean, , is an unbiased estimator of the population mean, . In symbols, . On the other hand, since 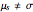, the sample standard deviation, , gives a biased estimate of .

[more]

For a small population of positive integers, this Demonstration illustrates unbiased versus biased estimators by displaying all possible samples of a given size, the corresponding sample statistics, the mean of the sampling distribution, and the value of the parameter. Note: for the sample proportion, it is the proportion of the population that is even that is considered.

[less]

Contributed by: Marc Brodie (Wheeling Jesuit University) (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

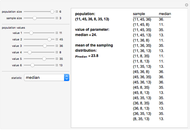
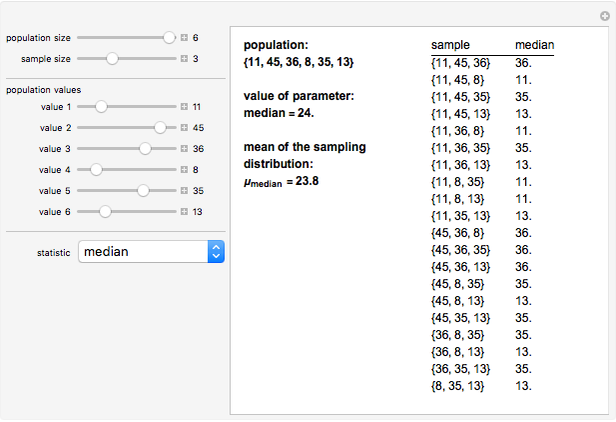
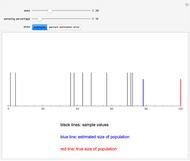
Snapshots 4 and 5 illustrate the fact that even if a statistic (in this case the median) is not an unbiased estimator of the parameter, it is possible for the mean of the sampling distribution to equal the value of the parameter for a specific population.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send