Understanding Runge-Kutta
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
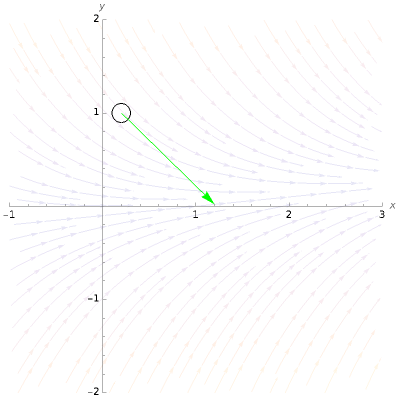
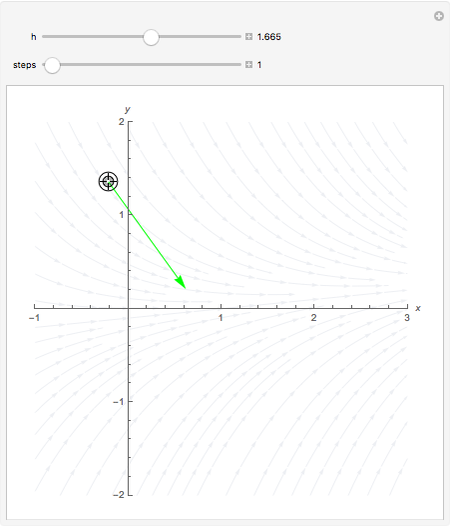
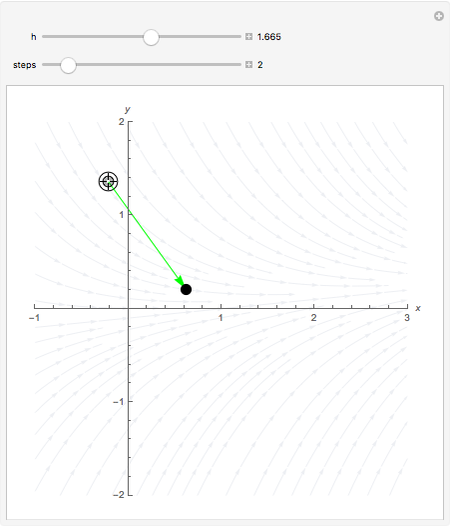
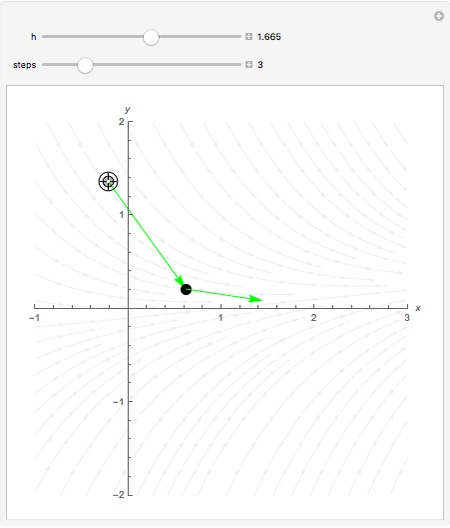
This Demonstration shows the steps involved in computing the Runge–Kutta method of integrating a differential equation and how the approximations behave. in the graphic, drag the locator (from which the calculations start), change the step length 
, and move through the steps in the calculation.
Contributed by: Gerrard Liddell (March 2011)
Open content licensed under CC BY-NC-SA
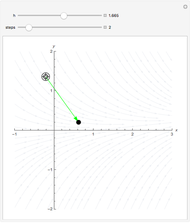
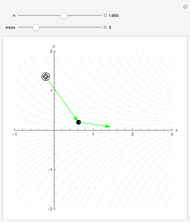
Snapshots
Details
Moving the initial point and varying the step size shows how, by sampling from points that contain the expected trajectory, the Runge–Kutta method improves on the Euler and related methods. Larger step sizes show how the method can err, while decreasing the step size shows the rapid convergence to the actual trajectory.
Permanent Citation
"Understanding Runge-Kutta"
http://demonstrations.wolfram.com/UnderstandingRungeKutta/
Wolfram Demonstrations Project
Published: March 7 2011
Global and Local Errors in Runge-Kutta Methods
Luis Rández
Numerical Methods for Differential Equations
Edda Eich-Soellner
Comparing Leapfrog Methods with Other Numerical Methods for Differential Equations
Ulrich Mutze
Integrating across Singularities
Ulrich Mutze
Euler's Method for the Exponential Function
Arnaud Crouzet
Runge-Kutta versus Velocity-Verlet Solutions for the Classical Harmonic Oscillator
Luigi Tiburzi
Boole Differential Equation with Continued Fractions
Andreas Lauschke
The Asynchronous Leapfrog Method as a Stiff ODE Solver
Ulrich Mutze
A Domain Decomposition Method with Orthogonal Collocation
Housam Binous
Picard's Method for Ordinary Differential Equations
Oliver K. Ernst
