Using Eigenvalue Analysis to Rotate in 3D

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
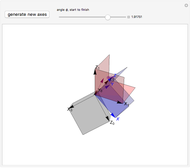
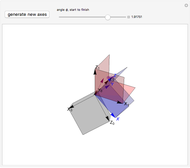
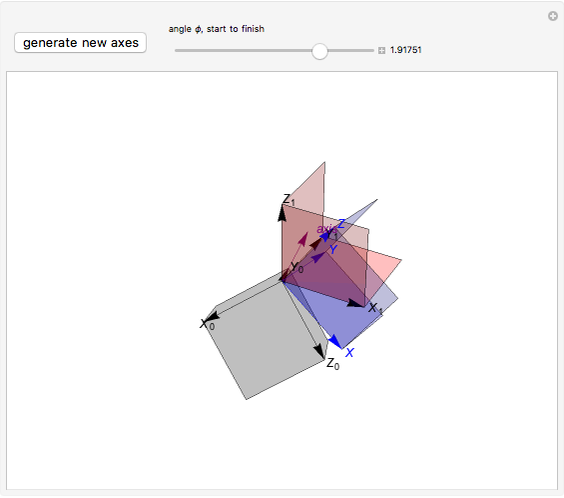
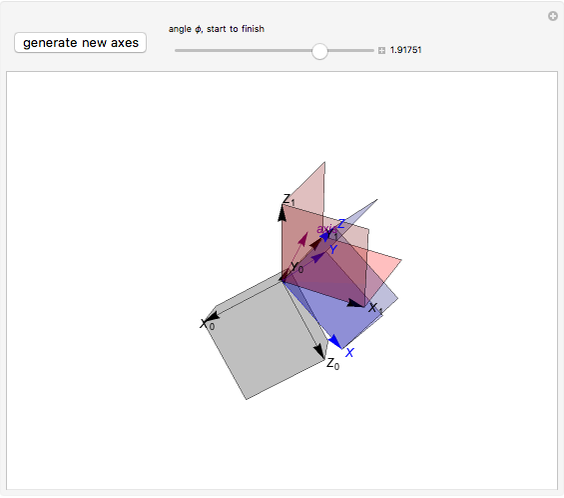
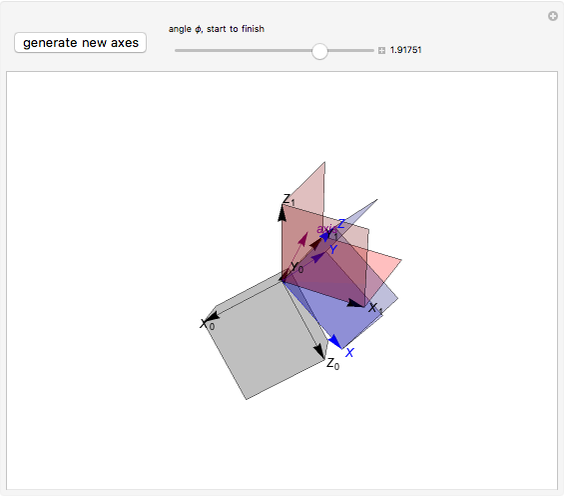
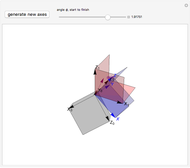
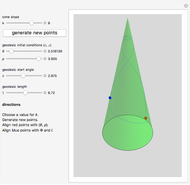
The continuous rotation of one right-handed coordinate system into another depends on the axis of rotation, the angle, and the sense of rotation. All these can be obtained from the eigenvalues and vectors of the change of basis matrix. (The matrix inverse gives only the end state of the rotation.) This Demonstration shows the axis of rotation and a slider that governs the rotation.
Contributed by: Raja Kountanya (December 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details

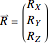 ,
,
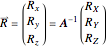 .
.
The process [1] involves finding the eigenvalues and eigenvectors of 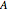 . The eigenvector corresponding to the eigenvalue of 1 gives the axis
. The eigenvector corresponding to the eigenvalue of 1 gives the axis  ; it is the only eigenvector whose components are all real. The two other eigenvalues are
; it is the only eigenvector whose components are all real. The two other eigenvalues are 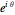 and
and 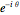 , whose eigenvectors are complex.
, whose eigenvectors are complex.
Therefore, by suitably ordering the eigenvalues and eigenvectors with the real part of the eigenvalues, the vector  can be deduced. That is,
can be deduced. That is,  is the eigenvector of the eigenvalue whose real part is the maximum.
is the eigenvector of the eigenvalue whose real part is the maximum.
The value  is given by
is given by
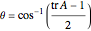 .
.
Suppose the sense of rotation is defined in the direction of  using the value
using the value  defined as follows:
defined as follows:
 .
.
Take one of the complex eigenvectors 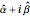 and let
and let  . Then
. Then
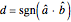 .
.
In this Demonstration, a random right-handed 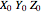 coordinate system with gray planes is first generated. (You can generate a new
coordinate system with gray planes is first generated. (You can generate a new 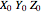 system to see different cases.) The fixed
system to see different cases.) The fixed 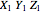 system (red axes and planes) is generated by taking the inverse of the column matrix
system (red axes and planes) is generated by taking the inverse of the column matrix 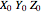 . Use the
. Use the  slider to continuously rotate the
slider to continuously rotate the 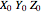 system (blue axes and planes) about the vector
system (blue axes and planes) about the vector  (purple) into the
(purple) into the 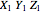 system.
system.
Reference
[1] L. Sadun. Rotation in 3 Dimensions [Video]. (Nov 21, 2014) www.youtube.com/watch?v=5BtDR25TE8k.
Permanent Citation