Using Zeta Zeros to Compute a Summatory Liouville Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
An important function in number theory is  , the number of integers in the range
, the number of integers in the range 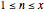 that have an even number of prime factors minus the number of integers in that range that have an odd number of prime factors. This function is nicely expressible as a sum of values of Liouville's function:
that have an even number of prime factors minus the number of integers in that range that have an odd number of prime factors. This function is nicely expressible as a sum of values of Liouville's function: 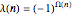 , where
, where 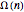 is the number or prime factors of
is the number or prime factors of  , via
, via 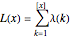 .
.
Contributed by: Robert Baillie (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
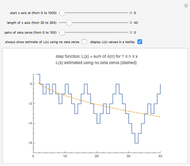
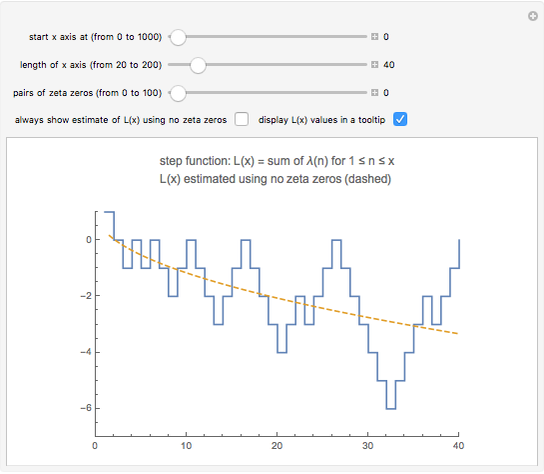
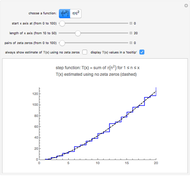
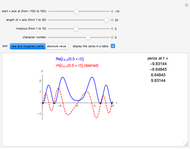
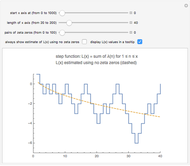
Snapshot 1: the graphs of the step function  and the formula using no zeta zeros
and the formula using no zeta zeros
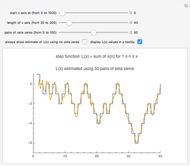
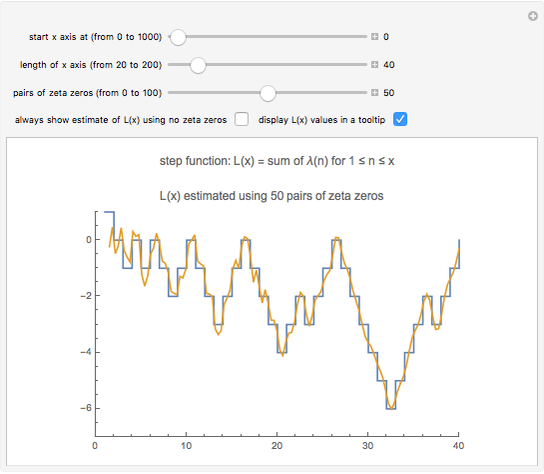
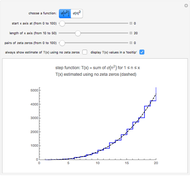
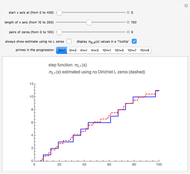
Snapshot 2: the graphs of  and the formula using 50 pairs of zeta zeros
and the formula using 50 pairs of zeta zeros
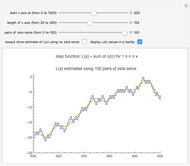
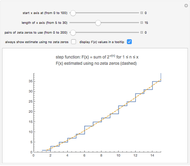
Snapshot 3:  for
for 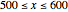 , showing that
, showing that 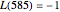 ,
, 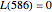 , and
, and 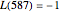 . It is surprising that
. It is surprising that 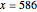 is the last
is the last  for which
for which 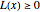 until
until 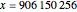 .
.
In number theory, we define 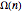 (capital omega) to be the number of prime factors of
(capital omega) to be the number of prime factors of  , counting multiplicity. Therefore,
, counting multiplicity. Therefore, 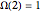 ,
, 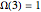 ,
, 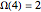 ,
, 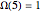 , and
, and 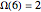 . The Liouville lambda function
. The Liouville lambda function 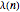 is defined to be
is defined to be  . So,
. So, 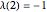 ,
,  ,
, 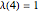 ,
, 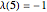 , and
, and 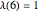 .
.
The function  is defined to be the sum of
is defined to be the sum of 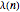 for
for 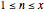 . Whenever
. Whenever  has an even number of prime factors (counting multiplicity), that
has an even number of prime factors (counting multiplicity), that  contributes
contributes  to the sum. Whenever
to the sum. Whenever  has an odd number of prime factors, that
has an odd number of prime factors, that  contributes
contributes 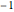 to the sum. This means that
to the sum. This means that  is the number of integers in the range
is the number of integers in the range 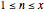 that have an even number of prime factors, minus the number that have an odd number of prime factors.
that have an even number of prime factors, minus the number that have an odd number of prime factors.
This Demonstration uses the following formula to calculate  :
:
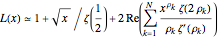 ,
,
where 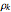 is the
is the 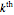 complex zero of the Riemann zeta function.
complex zero of the Riemann zeta function.
If you use the slider to choose, say, one pair of zeta zeros, then the first sum in the above formula, in effect, combines two terms corresponding to the first conjugate pair of zeta zeros  and
and 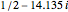 . So, when these terms are added, their imaginary parts cancel while their real parts add. The
. So, when these terms are added, their imaginary parts cancel while their real parts add. The 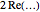 applied to the first sum is simply an efficient way to combine the two terms for each pair of zeta zeros.
applied to the first sum is simply an efficient way to combine the two terms for each pair of zeta zeros.
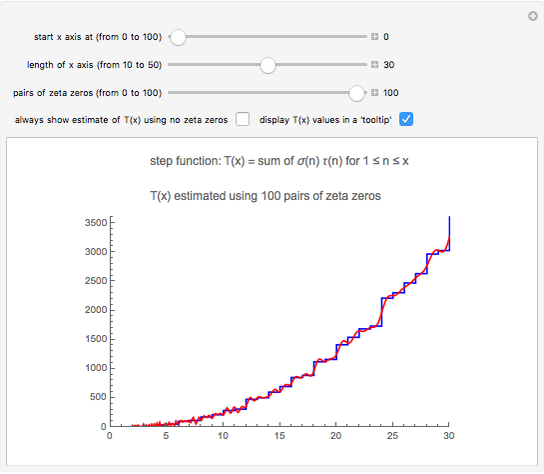
The dominant part of the formula is 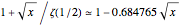 . As
. As  increases, this expression becomes more and more negative. This means that it must be the sum involving zeta zeros that causes the graph of
increases, this expression becomes more and more negative. This means that it must be the sum involving zeta zeros that causes the graph of  to fluctuate.
to fluctuate.
For example, at 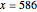 ,
, 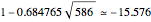 . But when we include 100 zeta zeros, the above formula gives the value
. But when we include 100 zeta zeros, the above formula gives the value 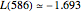 , which is much closer to the exact value,
, which is much closer to the exact value, 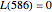 . We could get even closer to this exact value by taking larger values of
. We could get even closer to this exact value by taking larger values of 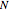 in the above formula.
in the above formula.
You can see from the graphs that for small 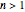 ,
, 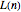 is less than or equal to zero. In 1919, the mathematician George Pólya conjectured that
is less than or equal to zero. In 1919, the mathematician George Pólya conjectured that 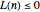 for all
for all 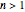 . However, in 1958, this conjecture was proven to be false. We now know that the smallest counterexample
. However, in 1958, this conjecture was proven to be false. We now know that the smallest counterexample 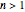 for which
for which 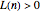 is
is 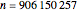 . In fact,
. In fact, 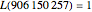 .
.
All known zeta zeros have multiplicity 1, which is assumed in the formula. At those values of  where
where  jumps from
jumps from  to
to 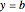 , the formula converges to the midpoint,
, the formula converges to the midpoint, 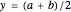 , as
, as 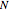 approaches infinity. You can see this in the graphs.
approaches infinity. You can see this in the graphs.
As we include more zeta zeros in the first sum, we more closely replicate the jumps in the step function  . This means that the zeros of the Riemann zeta function somehow "know" how many prime factors each of the integers has.
. This means that the zeros of the Riemann zeta function somehow "know" how many prime factors each of the integers has.
To prove formulas like the one above, see [3]. The key is to apply Perron's formula to the following identity, which holds for  :
:
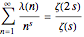 .
.
This identity is found in [2], or it may be derived (in Mathematica Version 7 or higher) from
DirichletTransform[LiouvilleLambda[n], n, s].
References:
[1] X. Gourdon, "The 10^13 First Zeros of the Riemann Zeta Function, and Zeros Computation at Very Large Height."
[2] G. H. Hardy and E. M. Wright, An Introduction to the Theory of Numbers, 4th ed., Oxford: Oxford University Press, 1965 p. 255.
[3] H. L. Montgomery and R. C. Vaughan, Multiplicative Number Theory: I. Classical Theory, Cambridge: Cambridge University Press, 2007 p. 397.
Permanent Citation