Using Zeta Zeros to Tally Squarefree Divisors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
For a positive integer  ,
, 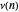 is the number of distinct prime factors of
is the number of distinct prime factors of 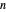 . The number of squarefree divisors of
. The number of squarefree divisors of 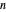 is
is  . We define
. We define  to be the sum of
to be the sum of 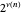 for positive integers
for positive integers 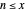 . The graph of
. The graph of 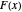 is an irregular step function.
is an irregular step function.
Contributed by: Robert Baillie (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
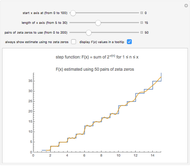
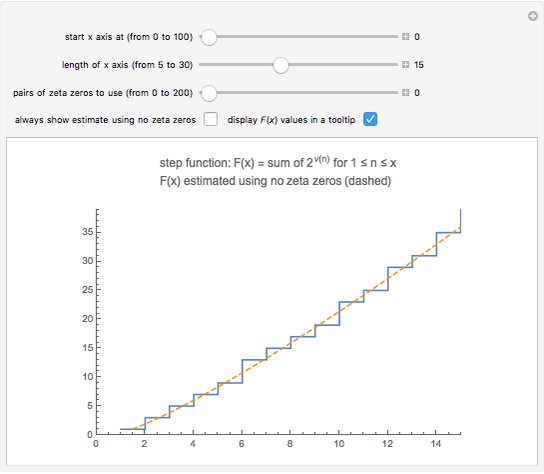
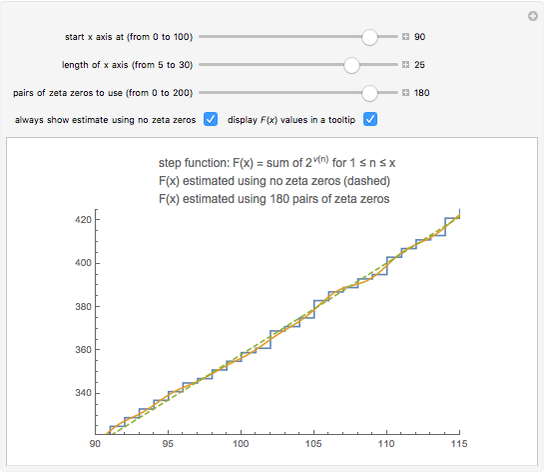
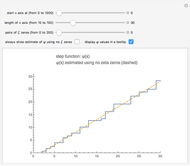
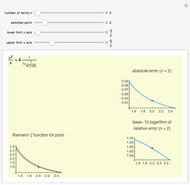
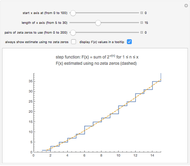
Snapshot 1: the graphs of the step function  and the formula using no zeta zeros
and the formula using no zeta zeros
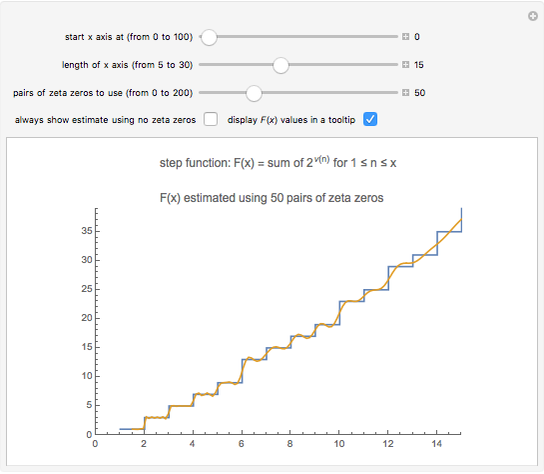
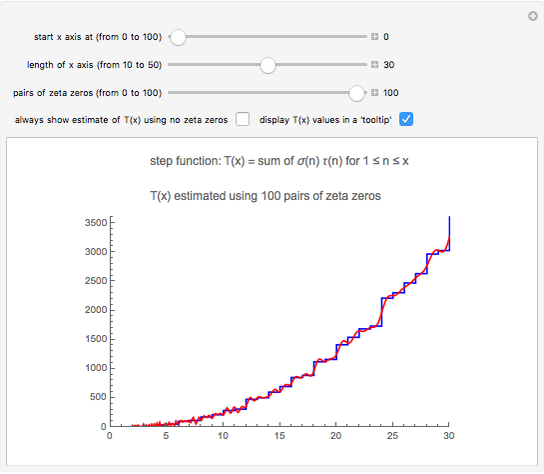
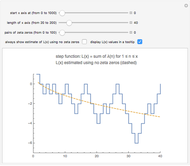
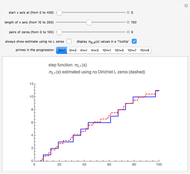
Snapshot 2: the graphs of 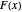 and the formula using 50 pairs of zeta zeros
and the formula using 50 pairs of zeta zeros
We call an integer "squarefree" if it is not divisible by the square of any prime. The first ten squarefree numbers are 1, 2, 3, 5, 6, 7, 10, 11, 13, and 14.
The function 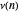 denotes the number of distinct prime factors of
denotes the number of distinct prime factors of 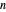 . For any
. For any 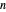 , the number of divisors of
, the number of divisors of 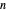 that are squarefree is
that are squarefree is 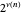 . This example shows why:
. This example shows why:  , because 60 has three distinct prime factors, which are 2, 3, and 5. We can list all the squarefree divisors of 60 by taking all
, because 60 has three distinct prime factors, which are 2, 3, and 5. We can list all the squarefree divisors of 60 by taking all 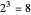 combinations of the presence or absence of the three primes (
combinations of the presence or absence of the three primes ( , where
, where 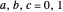 ):
):
1
2
3
5
2×3
2×5
3×5
2×3×5
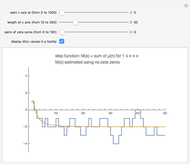
The sum of 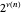 over positive integers
over positive integers 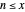 is a function of
is a function of 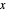 that we denote by
that we denote by 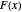 .
. 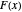 is an increasing, but irregular, step function.
is an increasing, but irregular, step function.
This Demonstration uses the following formula to calculate 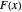 :
:
(1) 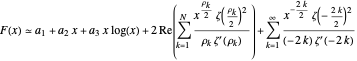 ,
,
where 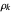 is the
is the 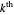 complex ("nontrivial") zero of the Riemann zeta function ζ(s). In this equation,
complex ("nontrivial") zero of the Riemann zeta function ζ(s). In this equation,
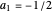 ,
,
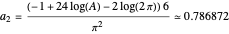 , where
, where 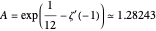 is Glaisher's constant, and
is Glaisher's constant, and
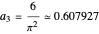 .
.
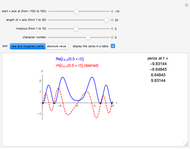
The first three complex zeros of the zeta function are approximately 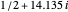 ,
, 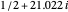 , and
, and 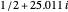 . The zeros occur in conjugate pairs, so if
. The zeros occur in conjugate pairs, so if 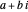 is a zero, then so is
is a zero, then so is 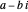 . The important Riemann hypothesis is the unproven conjecture that all these complex zeros have real part 1/2. So far, it has been verified that the first
. The important Riemann hypothesis is the unproven conjecture that all these complex zeros have real part 1/2. So far, it has been verified that the first 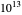 complex zeros do, indeed, have real part 1/2 (see [1]).
complex zeros do, indeed, have real part 1/2 (see [1]).
If you use the slider to choose, say, 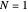 pair of zeta zeros, then the first sum in the above formula, in effect, combines two terms corresponding to the first pair of zeta zeros
pair of zeta zeros, then the first sum in the above formula, in effect, combines two terms corresponding to the first pair of zeta zeros  and
and 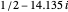 . These two terms are conjugates of each other. So, when these terms are added, their imaginary parts cancel while their real parts add. The
. These two terms are conjugates of each other. So, when these terms are added, their imaginary parts cancel while their real parts add. The 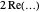 applied to the first sum is simply an efficient way to combine the two terms for each pair of zeta zeros.
applied to the first sum is simply an efficient way to combine the two terms for each pair of zeta zeros.
Notice that the second sum has the same form as the first, except that the second sum extends over the so-called "trivial" zeros of the zeta function, namely, 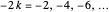 . The second sum is small when
. The second sum is small when 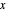 is large. The dominant terms in the formula are
is large. The dominant terms in the formula are 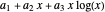 . If you use the slider to choose "no zeta zeros", this is the estimate of
. If you use the slider to choose "no zeta zeros", this is the estimate of 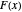 that is plotted. This expression is fairly close to
that is plotted. This expression is fairly close to 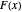 , but the accuracy of the formula improves as we include terms with zeta zeros. This Demonstration shows that the zeros of the zeta function somehow carry information about the squarefree divisors of the integers.
, but the accuracy of the formula improves as we include terms with zeta zeros. This Demonstration shows that the zeros of the zeta function somehow carry information about the squarefree divisors of the integers.
All known zeta zeros have multiplicity 1. The above formula assumes that all zeta zeros have multiplicity 1. At those values of  where
where 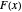 jumps from
jumps from 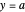 to
to  , the above formula converges to the midpoint,
, the above formula converges to the midpoint, 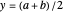 , as
, as 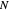 approaches infinity.
approaches infinity.
Where Does Equation 1 Come From?
Page 397 of reference [3] shows how to use Perron's formula to prove equation (1). Perron's formula ([3], p. 137) says that if the series
(2) 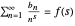
converges for 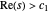 , then we can express the sum of
, then we can express the sum of 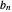 , for
, for 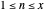 , as an integral:
, as an integral:
(3) 
where 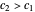 . By Cauchy's residue theorem, the value of this integral can be calculated by summing the residues of the integrand.
. By Cauchy's residue theorem, the value of this integral can be calculated by summing the residues of the integrand.
To prove equation (1), we start with this identity, which holds for 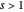 :
:
(4) 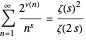 .
.
This can be found on page 255 of [2]. We now apply Perron's formula with  and
and  . We shift the integration contour to the left to include the residues listed below. The residues arise from the values of
. We shift the integration contour to the left to include the residues listed below. The residues arise from the values of  where the numerator of the integrand has a pole, or where the denominator is 0.
where the numerator of the integrand has a pole, or where the denominator is 0.
In formula (1) above, 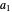 comes from the residue of
comes from the residue of 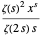 at
at 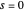 . The expression
. The expression 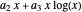 comes from the residue at
comes from the residue at 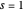 , where the numerator
, where the numerator 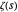 has a pole. The first sum in equation (1) is the sum of the residues at the nontrivial zeros of
has a pole. The first sum in equation (1) is the sum of the residues at the nontrivial zeros of 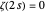 . (
. (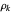 is the
is the 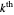 nontrivial zero of
nontrivial zero of 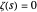 , so
, so  is the
is the 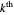 zero of
zero of 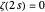 ). The second sum comes from the trivial zeros of
). The second sum comes from the trivial zeros of 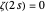 . In analytic number theory, formula (1) is known as an "explicit formula"; there are others in the last six related links.
. In analytic number theory, formula (1) is known as an "explicit formula"; there are others in the last six related links.
References:
[1] X. Gourdon, "The 10^13 First Zeros of the Riemann Zeta Function, and Zeros Computation at Very Large Height."
[2] G. H. Hardy and E. M. Wright, An Introduction to the Theory of Numbers, 4th ed., Oxford: Oxford University Press, 1965.
[3] H. L. Montgomery and R. C. Vaughan, Multiplicative Number Theory: I. Classical Theory, Cambridge: Cambridge University Press, 2007.
Permanent Citation