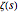Using Zeta Zeros to Tally the Euler Phi Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The Euler phi ( ) function (also called the totient function) is important in number theory;
) function (also called the totient function) is important in number theory; 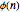 is the number of positive integers less than or equal to
is the number of positive integers less than or equal to  that have no factor in common with
that have no factor in common with  . For example,
. For example, 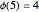 and
and 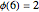 .
.
Contributed by: Robert Baillie (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
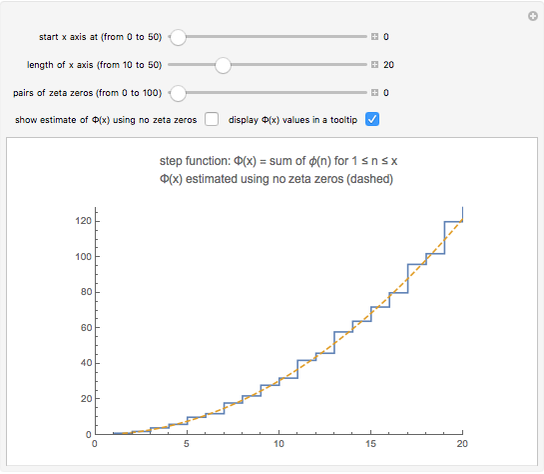
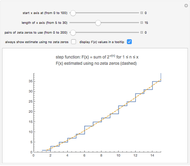
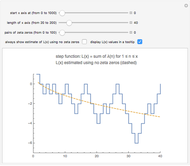
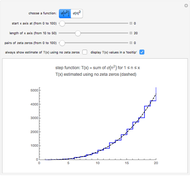
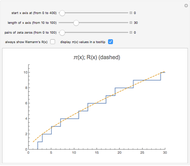
Snapshot 1: the graphs of the step function 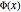 and the formula using no zeta zeros
and the formula using no zeta zeros
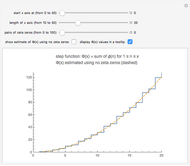
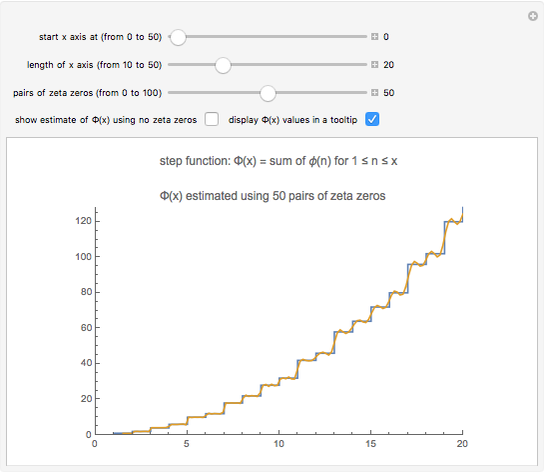
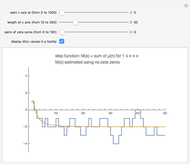
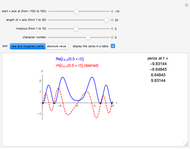
Snapshot 2: the graphs of 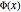 and the formula using 30 pairs of zeta zeros
and the formula using 30 pairs of zeta zeros
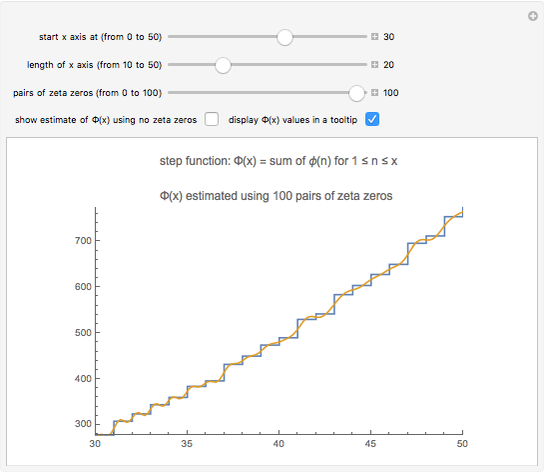
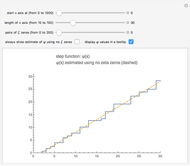
Snapshot 3: for larger  , we need more and more zeta zeros in order to closely match the step function
, we need more and more zeta zeros in order to closely match the step function
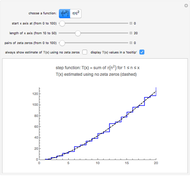
This Demonstration uses the following formula to calculate 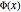 :
:
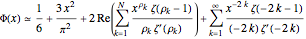 ,
,
where 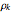 is the
is the 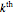 complex zero of the Riemann zeta function.
complex zero of the Riemann zeta function.
The first three complex zeros of the zeta function are approximately 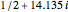 ,
, 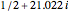 , and
, and  . The zeros occur in conjugate pairs, so if
. The zeros occur in conjugate pairs, so if 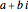 is a zero, then so is
is a zero, then so is 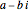 . The important Riemann hypothesis is the unproven conjecture that all these complex zeros have real part 1/2. So far, it has been verified that the first
. The important Riemann hypothesis is the unproven conjecture that all these complex zeros have real part 1/2. So far, it has been verified that the first 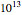 complex zeros do, indeed, have real part 1/2 (see [1]).
complex zeros do, indeed, have real part 1/2 (see [1]).
If you use the slider to choose, say, one pair of zeta zeros, then the first sum in the above formula, in effect, combines two terms corresponding to the first conjugate pair of zeta zeros 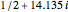 and
and 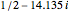 . So, when these terms are added, their imaginary parts cancel while their real parts add. The
. So, when these terms are added, their imaginary parts cancel while their real parts add. The 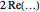 applied to the first sum is simply an efficient way to combine the two terms for each pair of zeta zeros.
applied to the first sum is simply an efficient way to combine the two terms for each pair of zeta zeros.
Notice that the second sum has the same form as the first, except that the second sum extends over the so-called "trivial" zeros of the zeta function, namely, 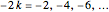 . The second sum is small when
. The second sum is small when  is large.
is large.
The dominant terms in the formula are 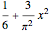 . This expression is fairly close to
. This expression is fairly close to 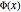 , but the accuracy of the formula improves as we include more terms with zeta zeros.
, but the accuracy of the formula improves as we include more terms with zeta zeros.
All known zeta zeros have multiplicity 1, which is assumed in the formula. At those values of  where
where 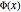 jumps from
jumps from  to
to 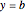 , the formula converges to the midpoint,
, the formula converges to the midpoint,  , as
, as 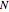 approaches infinity. You can see this in the graphs.
approaches infinity. You can see this in the graphs.
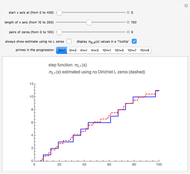
Also, you can use the tooltip to read off individual  values from the graph. The definition of
values from the graph. The definition of 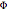 means that
means that 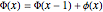 . So, for example, at
. So, for example, at 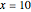 , the graph jumps from 28 to 32; this increase is simply
, the graph jumps from 28 to 32; this increase is simply 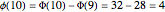 .
.
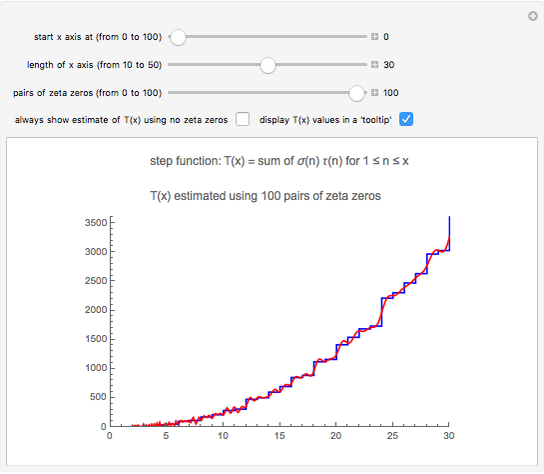
To prove formulas like the one for  , see [3]. The key is to apply Perron's formula to the following identity, which holds for
, see [3]. The key is to apply Perron's formula to the following identity, which holds for  :
:
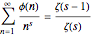 .
.
This identity is in [2], or it may be derived (in Mathematica Version 7 or higher) from
DirichletTransform[EulerPhi[n], n, s].
References:
[1] X. Gourdon, "The 10^13 First Zeros of the Riemann Zeta Function, and Zeros Computation at Very Large Height."
[2] G. H. Hardy and E. M. Wright, The Theory of Numbers, 4th ed., Oxford: Oxford University Press, 1965 p. 250.
[3] H. L. Montgomery and R. C. Vaughan, Multiplicative Number Theory: I. Classical Theory, Cambridge: Cambridge University Press, 2007 p. 397.
Permanent Citation