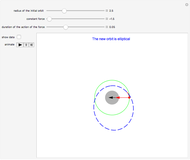
Usual and Unusual Pendulums

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
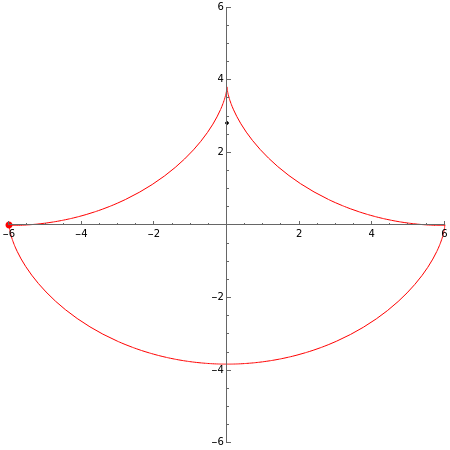
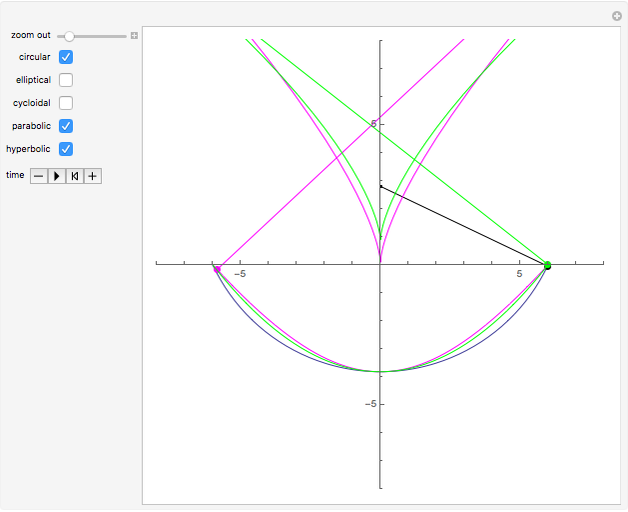
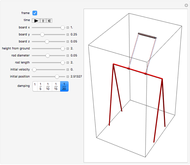
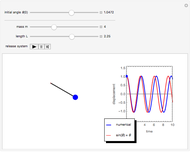
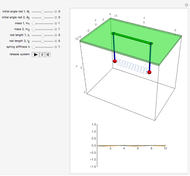
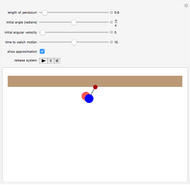
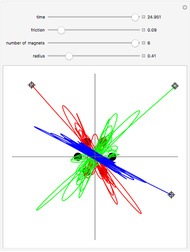
A pendulum can be defined as a bob hanging from a string whose other end is attached to a fixed point. When the bob is displaced from its equilibrium position and set free, it will move back and forth along a circular path.
[more]
Contributed by: Stelios Kapranidis (March 2013)
Open content licensed under CC BY-NC-SA
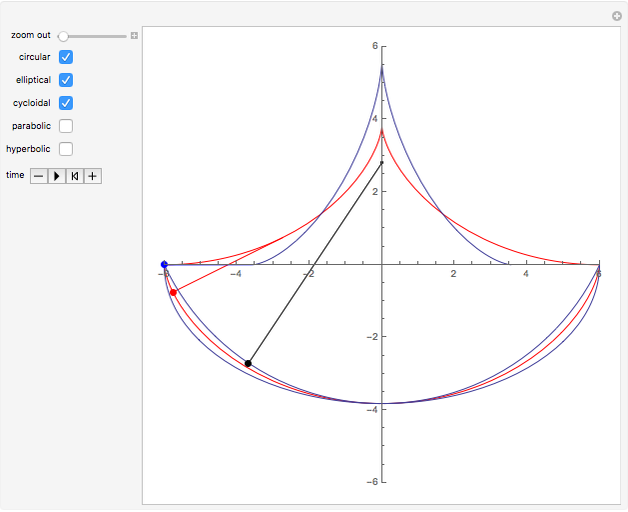
Snapshots
Details
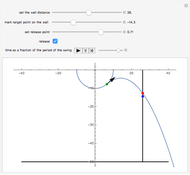
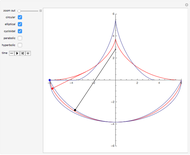
The evolute of a curve is defined as the locus of the centers of curvature of the curve. The evolute of a curve is important in the theory of the pendulum because of the property expressed by the following theorem (see [1], p. 312).
If 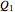 and
and 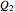 are the centers of curvature corresponding to the points
are the centers of curvature corresponding to the points  and
and 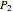 of a curve, the length of the arc of the evolute between
of a curve, the length of the arc of the evolute between 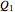 and
and 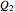 is equal to the difference between the radii of curvature at
is equal to the difference between the radii of curvature at  and
and 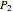 .
.
The evolute of the orbit of a pendulum can be calculated in the following way (see e.g. [2], p. 79). If 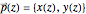 is a parametric equation of the orbit of a pendulum, the unit tangent vector
is a parametric equation of the orbit of a pendulum, the unit tangent vector 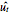 of
of  at any
at any  is given by:
is given by:
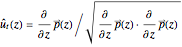 .
.
The curvature of  at any
at any  is given by the magnitude of the vector:
is given by the magnitude of the vector:
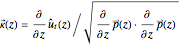 ,
,
while for each  the center of curvature can be located by the vector:
the center of curvature can be located by the vector:
 .
.
It is interesting to note that from this definition we find that the evolute of a circle consists of a single point, the center of the circle.
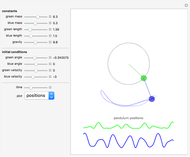
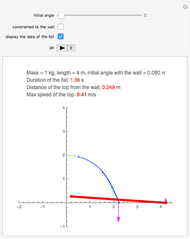
To describe the motion of a pendulum, we need to derive a function 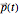 that gives the position
that gives the position  of the pendulum at any time
of the pendulum at any time  . Since the motion of a pendulum is periodic, we only need to know the period
. Since the motion of a pendulum is periodic, we only need to know the period 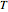 of the pendulum and the function
of the pendulum and the function 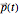 for
for 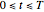 . The function
. The function 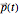 can be derived on the basis of the principle of conservation of mechanical energy (see e.g. [1], p. 309). The calculations for this Demonstration are done numerically using standard Mathematica functions.
can be derived on the basis of the principle of conservation of mechanical energy (see e.g. [1], p. 309). The calculations for this Demonstration are done numerically using standard Mathematica functions.
The principle of conservation of mechanical energy requires that the kinetic energy of the pendulum at any instant be equal to the difference between its potential energy at the initial position and its potential energy at the current position. Assuming that a parametric equation of the orbit of a pendulum is 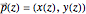 and that the endpoints of the orbit are
and that the endpoints of the orbit are  and
and 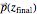 , we find:
, we find:

and
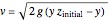 ,
,
where  is the acceleration of gravity.
is the acceleration of gravity.
If 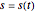 gives the arc length traveled by the bob as a function of time, then
gives the arc length traveled by the bob as a function of time, then
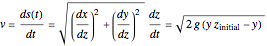
and
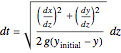 .
.
From this equation we find that the period 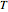 of the pendulum is
of the pendulum is
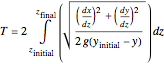 .
.
We also find that the time  it takes the bob to move from the initial position
it takes the bob to move from the initial position  to a position
to a position  is
is
 .
.
Since the motion of the bob is symmetric, we only need to establish a function that gives the time  for any
for any  only for the first half of the orbit, that is, for the first quarter of the period. By inverting this function we can obtain the functions
only for the first half of the orbit, that is, for the first quarter of the period. By inverting this function we can obtain the functions 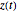 and
and 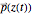 for
for 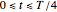 . Because of the symmetries in the motion of the bob, this function can be extended so that the function
. Because of the symmetries in the motion of the bob, this function can be extended so that the function 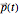 gives the position
gives the position  of the bob for any time
of the bob for any time  in
in 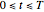 . Since the period of the bob can also be calculated as we indicate above, its position can be determined at any time
. Since the period of the bob can also be calculated as we indicate above, its position can be determined at any time  .
.
References
[1] G. F. Simmons, Calculus Gems: Brief Lives and Memorable Mathematics, New York: McGraw-Hill, 1992.
[2] B. Davis, H. Porta, and J. Uhl, Calculus & Mathematica: Vector Calculus: Measuring in Two and Three Dimensions, Reading, MA: Addison-Wesley Publishing Company, 1994.
Permanent Citation