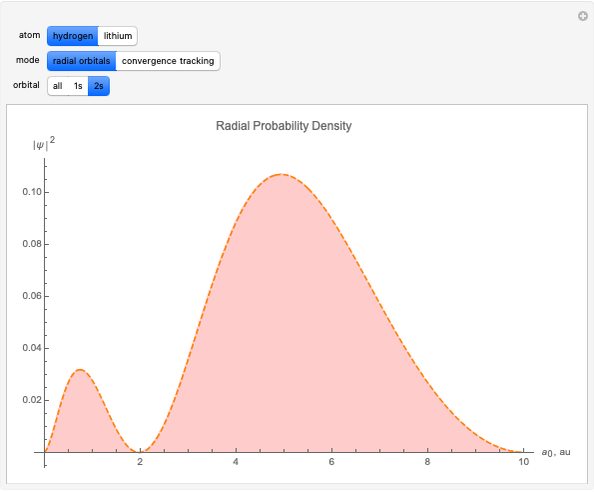
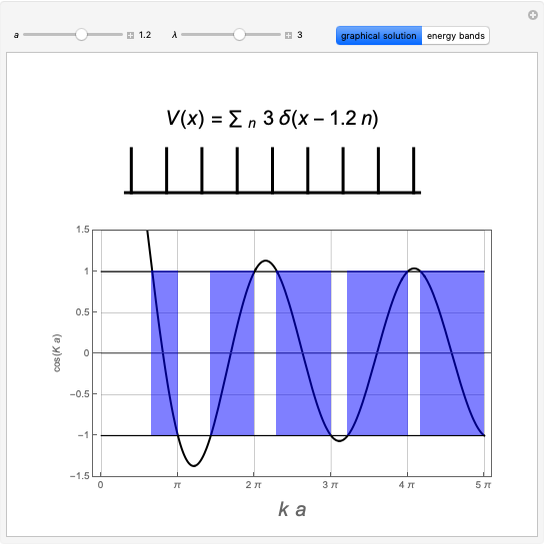
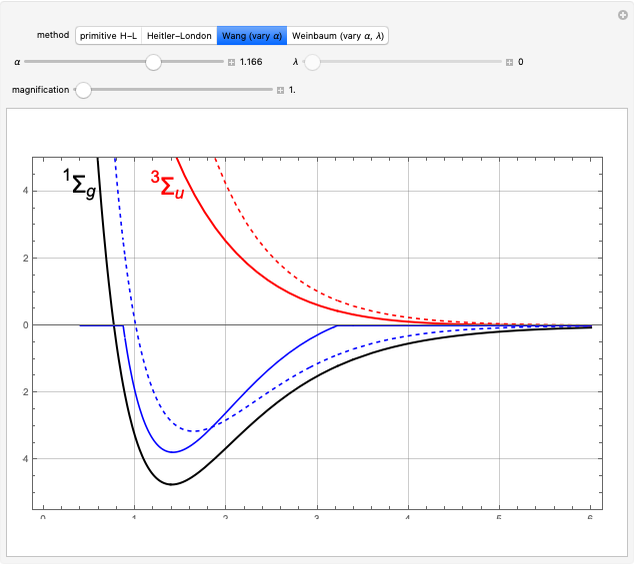
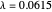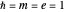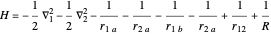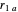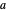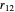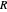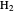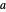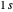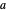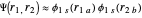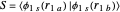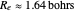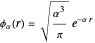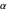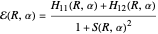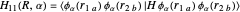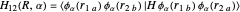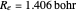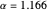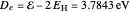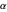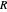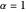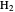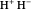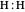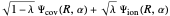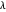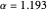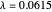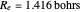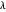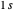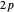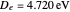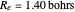The first successful explanation of chemical bonding using quantum mechanics was provided by the simple computation of Heitler and London on the hydrogen molecule 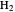 in 1927, only one year after the Schrödinger equation was proposed. This gave the first rational explanation of the chemical concept of the covalent electron-pair bond, proposed by G. N. Lewis in 1916 and Irving Langmuir in 1919. The hydrogen molecule has a binding energy of
in 1927, only one year after the Schrödinger equation was proposed. This gave the first rational explanation of the chemical concept of the covalent electron-pair bond, proposed by G. N. Lewis in 1916 and Irving Langmuir in 1919. The hydrogen molecule has a binding energy of 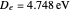 (not including the zero-point vibrational energy). This represents the minimum of the Born–Oppenheimer potential curve for
(not including the zero-point vibrational energy). This represents the minimum of the Born–Oppenheimer potential curve for 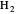 at an internuclear separation of
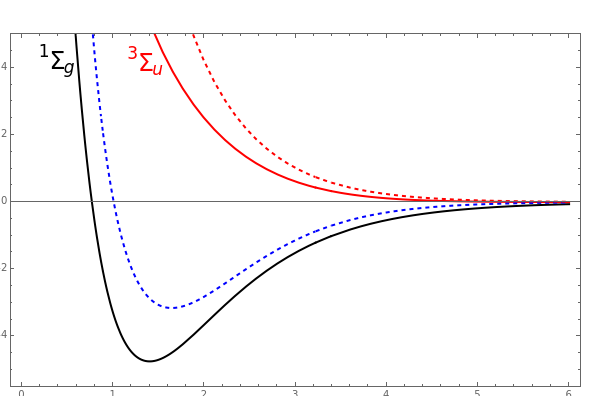
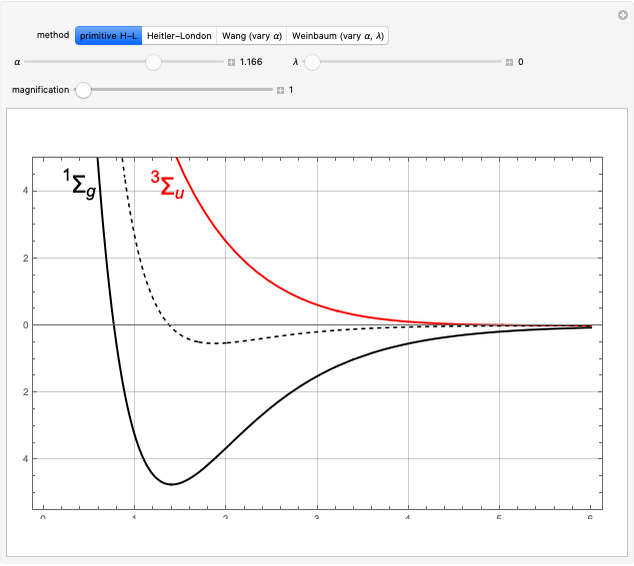
at an internuclear separation of 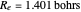 (0.7414Å). This is shown as a thick black curve representing the
(0.7414Å). This is shown as a thick black curve representing the 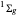 ground electronic state. As
ground electronic state. As 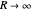 , the molecule dissociates into two hydrogen atoms in their
, the molecule dissociates into two hydrogen atoms in their 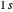 ground states, with antiparallel spins. Also shown, in red, is the antibonding
ground states, with antiparallel spins. Also shown, in red, is the antibonding 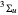 potential curve for two hydrogen atoms with parallel spins.
potential curve for two hydrogen atoms with parallel spins.
The Hamiltonian for the  molecule, within the Born–Oppenheimer approximation, consists of the kinetic energies of the two electrons added to six Coulombic potential-energy contributions. In atomic units (
molecule, within the Born–Oppenheimer approximation, consists of the kinetic energies of the two electrons added to six Coulombic potential-energy contributions. In atomic units (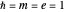 ):
):
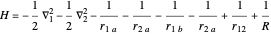 ,
,
where 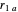 is the distance between electron 1 and proton
is the distance between electron 1 and proton 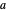 , and so fourth,
, and so fourth, 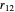 is the instantaneous distance between the two electrons, and
is the instantaneous distance between the two electrons, and 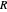 is the internuclear separation. Since the hydrogen molecule
is the internuclear separation. Since the hydrogen molecule 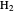 is formed from a combination of hydrogen atoms
is formed from a combination of hydrogen atoms 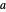 and
and  , one might consider as a primitive first approximation a product of hydrogen-atom
, one might consider as a primitive first approximation a product of hydrogen-atom 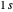 functions centered on protons
functions centered on protons 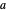 and
and  , respectively:
, respectively: 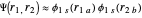 . This gives a binding energy
. This gives a binding energy  at a nuclear separation of
at a nuclear separation of  , indicating that the hydrogen atoms can indeed form a stable molecule. However, the calculated energy is over an order of magnitude too small to account for the strongly-bound hydrogen molecule.
, indicating that the hydrogen atoms can indeed form a stable molecule. However, the calculated energy is over an order of magnitude too small to account for the strongly-bound hydrogen molecule.
Heisenberg had suggested that a wavefunction should be symmetrical (or antisymmetrical) with respect to interchange of its electron labels, to take account of the indistinguishability of identical particles. Heitler and London [3] took this into account by adding a term to the wavefunction in which the electron labels are reversed. The approximate wavefunction with appropriate exchange symmetry can be written
 ≈
≈ ≈InlineMath[&straightpi;1s(r1a)&straightpi;1s(r2b)±&straightpi;1s(r1b)&straightpi;1s(r2a)]/2±2S2.
≈InlineMath[&straightpi;1s(r1a)&straightpi;1s(r2b)±&straightpi;1s(r1b)&straightpi;1s(r2a)]/2±2S2.
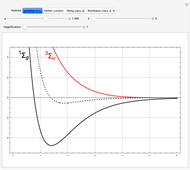
The function is normalized, with introduction of the overlap integral 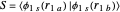 . The plus and minus signs apply to the bonding and repulsive states, respectively. The computed result (augmented by an integral evaluated by Sugiura [4]) gave a much more realistic binding energy value of 3.156 eV, with
. The plus and minus signs apply to the bonding and repulsive states, respectively. The computed result (augmented by an integral evaluated by Sugiura [4]) gave a much more realistic binding energy value of 3.156 eV, with 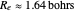 .
.
A further improvement was implemented by Wang [5], using scaled 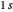 functions of the form
functions of the form 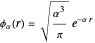 , with
, with 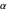 treated as a variational parameter chosen so as to minimize the molecular energy (rather than keeping
treated as a variational parameter chosen so as to minimize the molecular energy (rather than keeping  , as in the hydrogen atom). The variational energy can be expressed
, as in the hydrogen atom). The variational energy can be expressed 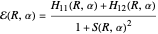 , with
, with 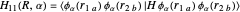 and
and 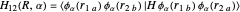 . The minimum is obtained at
. The minimum is obtained at 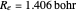 with
with 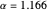 , giving a binding energy of
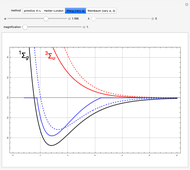
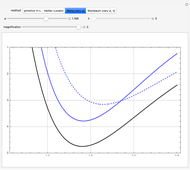
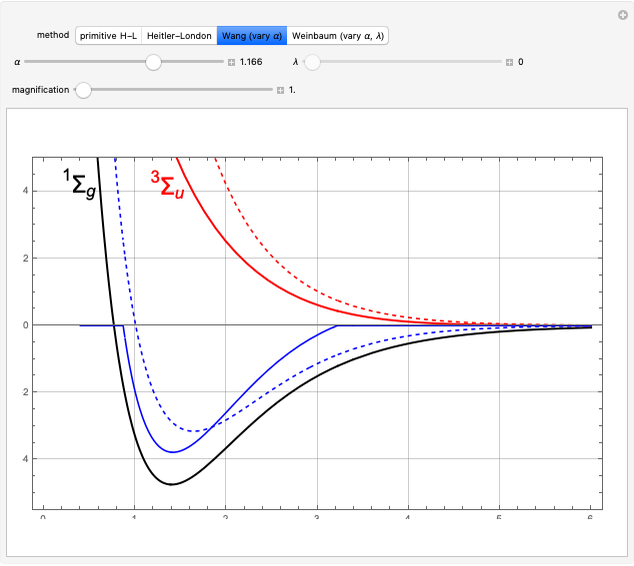
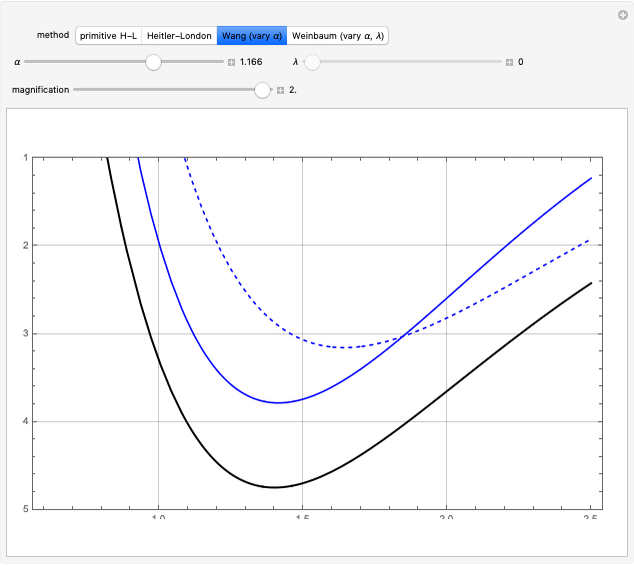
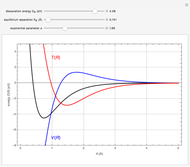
, giving a binding energy of 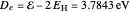 . With selection of the setter "Wang", the graphic shows solid blue curves for varying
. With selection of the setter "Wang", the graphic shows solid blue curves for varying 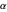 in the vicinity of the minimum in the potential curve. The energy values for a given
in the vicinity of the minimum in the potential curve. The energy values for a given  are not significant for any larger range of
are not significant for any larger range of 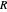 . Also shown, as a dashed blue curve, is the original Heitler–London computation, with
. Also shown, as a dashed blue curve, is the original Heitler–London computation, with 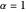 throughout.
throughout.
The last enhancement we consider explicitly is the inclusion of ionic-covalent resonance. Linus Pauling recognized that the "true" structure of a molecule such as 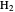 was actually a "resonance hybrid", an admixture of some ionic character
was actually a "resonance hybrid", an admixture of some ionic character 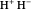 and
and  into the purely covalent structure
into the purely covalent structure 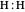 . Weinbaum [6] suggested a variational function of the form
. Weinbaum [6] suggested a variational function of the form 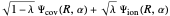 , to be optimized with respect to the two parameters
, to be optimized with respect to the two parameters 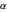 and
and 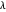 . You can generate the curve shown in green by varying these parameters. The optimum values are
. You can generate the curve shown in green by varying these parameters. The optimum values are 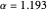 ,
, 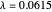 , yielding a binding energy of 4.024 eV at
, yielding a binding energy of 4.024 eV at 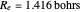 . This value
. This value 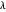 implies that inclusion of about 6% ionic structure optimizes the computation based on this function.
implies that inclusion of about 6% ionic structure optimizes the computation based on this function.
Further small improvements, which we do not enumerate, were obtained by consideration of "polarization" of each 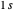 atomic function in the direction of the opposite atom by addition of some
atomic function in the direction of the opposite atom by addition of some 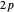 character.
character.
The plots shown can be magnified, to focus in on the region around the minimum.
The definitive computation on the hydrogen molecule, and in a sense an affirming verification of the validity of the many-particle Schrödinger equation, was the work of James and Coolidge [7]. They used a 13-term linear variational method based on prolate spheroidal (also known as confocal elliptical) coordinates to obtain the values 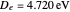 ,
, 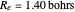 , within the known experimental values at the time. (This is a possible subject of a future Demonstration.) More recently, with the advent of high-powered computational capability, even more accurate results have been obtained, including a 100-parameter extension of Coolidge and James and corrections for the Born-Oppenheimer approximation and relativistic contributions.
, within the known experimental values at the time. (This is a possible subject of a future Demonstration.) More recently, with the advent of high-powered computational capability, even more accurate results have been obtained, including a 100-parameter extension of Coolidge and James and corrections for the Born-Oppenheimer approximation and relativistic contributions.
[less]

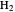 in 1927, only one year after the Schrödinger equation was proposed. This gave the first rational explanation of the chemical concept of the covalent electron-pair bond, proposed by G. N. Lewis in 1916 and Irving Langmuir in 1919. The hydrogen molecule has a binding energy of
in 1927, only one year after the Schrödinger equation was proposed. This gave the first rational explanation of the chemical concept of the covalent electron-pair bond, proposed by G. N. Lewis in 1916 and Irving Langmuir in 1919. The hydrogen molecule has a binding energy of 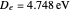 (not including the zero-point vibrational energy). This represents the minimum of the Born–Oppenheimer potential curve for
(not including the zero-point vibrational energy). This represents the minimum of the Born–Oppenheimer potential curve for 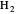 at an internuclear separation of
at an internuclear separation of 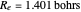 (0.7414Å). This is shown as a thick black curve representing the
(0.7414Å). This is shown as a thick black curve representing the 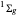 ground electronic state. As
ground electronic state. As 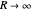 , the molecule dissociates into two hydrogen atoms in their
, the molecule dissociates into two hydrogen atoms in their 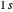 ground states, with antiparallel spins. Also shown, in red, is the antibonding
ground states, with antiparallel spins. Also shown, in red, is the antibonding 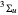 potential curve for two hydrogen atoms with parallel spins.
potential curve for two hydrogen atoms with parallel spins.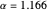
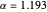 ,
,