Wolfram Demonstrations Project
7922

Van Aubel's Theorem for Quadrilaterals

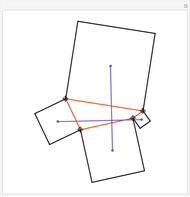
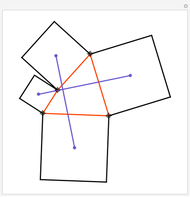
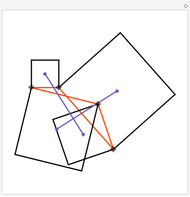
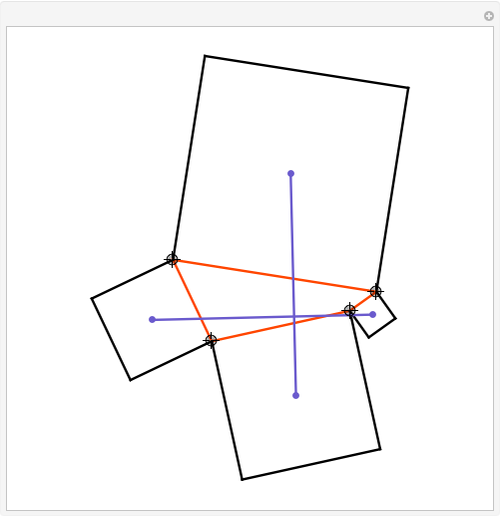
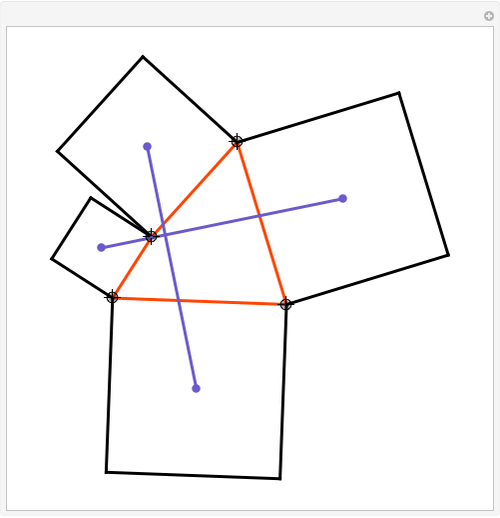
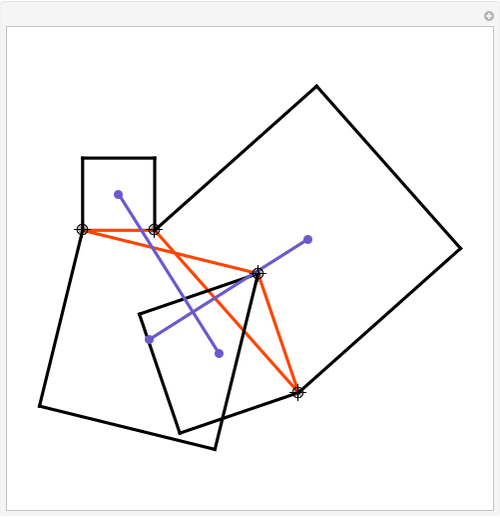
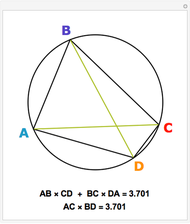
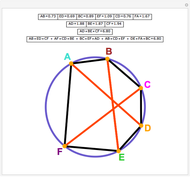
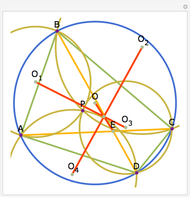
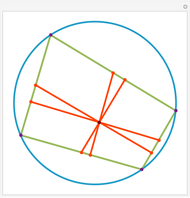
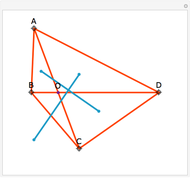
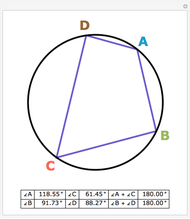
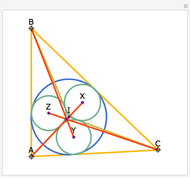
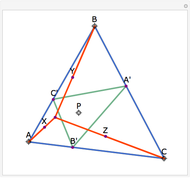
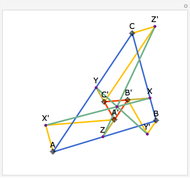
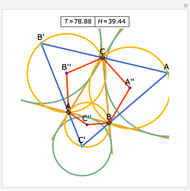
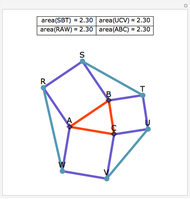
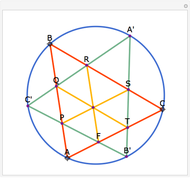
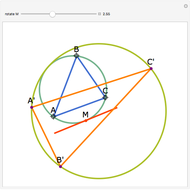
Construct squares on the outside of the four sides of a quadrilateral and draw lines between the centers of the opposite squares. Then the two lines have the same length and are perpendicular.

THINGS TO TRY

SNAPSHOTS

  • [Snapshot]
  • [Snapshot]
  • [Snapshot]

RELATED LINKS

PERMANENT CITATION

"Van Aubel's Theorem for Quadrilaterals" from the Wolfram Demonstrations Project
 http://demonstrations.wolfram.com/VanAubelsTheoremForQuadrilaterals/
Contributed by: Jay Warendorff




Related Topics




Contribute




 
RELATED RESOURCES
Mathematica »
 The #1 tool for creating Demonstrations
and anything technical. 		Wolfram|Alpha »
 Explore anything with the first
computational knowledge engine. 		MathWorld »
 The web's most extensive
mathematics resource. 		Course Assistant Apps »
 An app for every course—
right in the palm of your hand.
Wolfram Blog »
 Read our views on math,
science, and technology. 		Computable Document Format »
 The format that makes Demonstrations
(and any information) easy to share and interact with. 		STEM Initiative »
 Programs & resources for
educators, schools & students. 		Computerbasedmath.org »
 Join the initiative for modernizing
math education.
Powered by Wolfram Mathematica © 2012 Wolfram Demonstrations Project & Contributors  |  Terms of Use  |  Privacy Policy  |  RSS Give us your feedback
Note: To run this Demonstration you need Mathematica 7+ or the free Mathematica Player 7EX
Download or upgrade to Mathematica Player 7EX
I already have Mathematica Player or Mathematica 7+