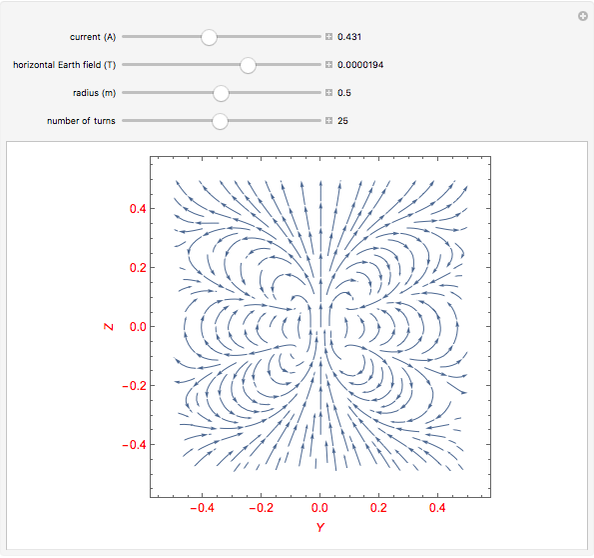
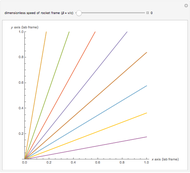
Vector Plot of Helmholtz Coil in Earth's Magnetic Field

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
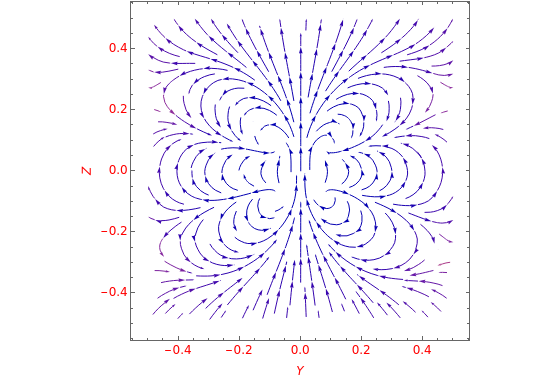
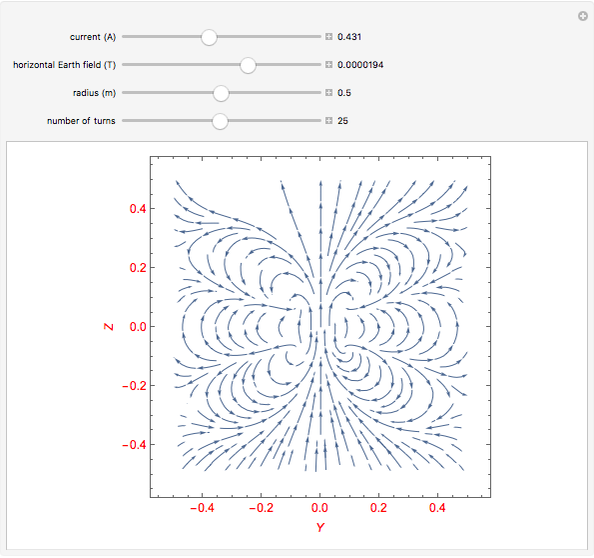
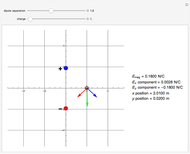
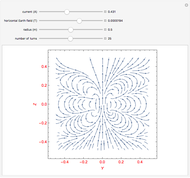
Even though a Helmholtz coil is used most often to cancel out the Earth's magnetic field, the Earth's and Helmholtz coil's magnetic field components may not cancel out uniformly over all space. This is of significance if you wish to know how a finite magnetic object might react and align itself with such a field. This Demonstration enables you to clearly see the non-uniformity and off-axis magnetic field components, thus allowing you to determine how such an object might react. The symmetry axis of the Helmholtz coil is aligned with the Earth's horizontal magnetic field. The coils are in the  -
- plane with one centered at
plane with one centered at 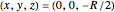 and the other separated by the radius
and the other separated by the radius 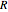 of the coils centered at
of the coils centered at 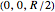 . The number of turns for the coils
. The number of turns for the coils 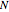 is initially set to 25 and the vacuum permeability
is initially set to 25 and the vacuum permeability  is included in the equations as well. You can vary the radius of the coils, the current supplied to them, the number of turns in the coils, and the Earth's field. All units are in the MKS system.
is included in the equations as well. You can vary the radius of the coils, the current supplied to them, the number of turns in the coils, and the Earth's field. All units are in the MKS system.
Contributed by: Cody A. Goolsby and Paul A. Nakroshis (November 2011)
(Department of Physics, University of Southern Maine, Portland, ME)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This present Demonstration gives a detailed understanding of the interactions between a magnetic torsion pendulum and the net horizontal magnetic field it feels while hanging at the nominal center of a Helmholtz coil pair used to cancel the horizontal component of the Earth's magnetic field. A Helmholtz coil, known for its ability to provide a relatively uniform magnetic field between its coils, is traditionally used to cancel out the Earth's magnetic field. With a Helmholtz coil suitably aligned so that the longitudinal axis of the coils points along the magnetic north-south direction, you can cancel the horizontal component of Earth's field (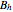 ) when sufficient current is supplied through its wires. At this critical current, even though you have succeeded in cancelling
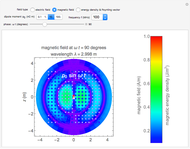
) when sufficient current is supplied through its wires. At this critical current, even though you have succeeded in cancelling 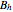 at the exact center of the coils, there remain small but non-zero, off-axis horizontal field components that can interact with a finite, imperfectly centered magnetic dipole. The above Demonstration gives this detailed rendering of the interplay between the Earth's field with the Helmholtz coil. The Demonstration thus allows you to see the net magnetic field vector plot anywhere between the two coils. Since the net field does not flip everywhere at once, you can see how the net field varies in space, in order to see how a finite magnetic object might react in such a field.
at the exact center of the coils, there remain small but non-zero, off-axis horizontal field components that can interact with a finite, imperfectly centered magnetic dipole. The above Demonstration gives this detailed rendering of the interplay between the Earth's field with the Helmholtz coil. The Demonstration thus allows you to see the net magnetic field vector plot anywhere between the two coils. Since the net field does not flip everywhere at once, you can see how the net field varies in space, in order to see how a finite magnetic object might react in such a field.
For a full derivation of the equations used to produce the vector plot, see [1].
For a more detailed discussion of a magnetic torsion pendulum interacting with the Helmholtz coil and Earth's field, see [2].
References
[1] C. Goolsby. "Finding the Magnetic Field from a Helmholtz Coil." Scribd. (Nov 16, 2011) www.scribd.com/fullscreen/72977243?access_key=key-2ly21ms0kg761vpsit6.
[2] C. Goolsby. "Rotational Behavior of a Magnetic Torsion Pendulum in a Helmholtz Coil." Scribd. (Nov 16, 2011) www.scribd.com/fullscreen/72977908?access_key=key-mqw1eunbsgg3citsfpc.
[3] Wikipedia. "Helmholtz Coil." (Oct 24, 2011) en.wikipedia.org/wiki/Helmholtz_coil.
[4] Wikipedia. "Earth's Magnetic Field." (Nov 23, 2011) en.wikipedia.org/wiki/Earth's_magnetic _field.
Permanent Citation