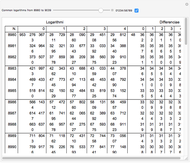
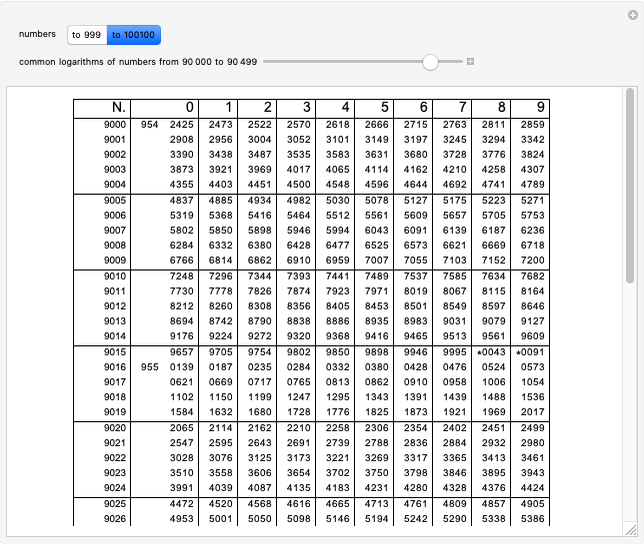
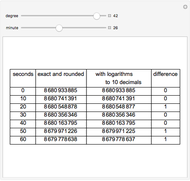
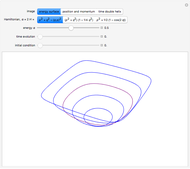
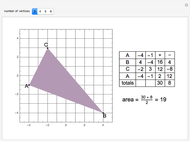
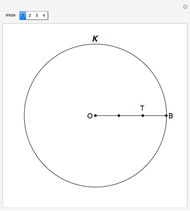
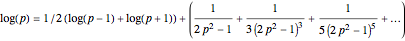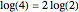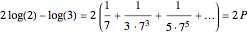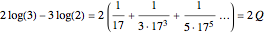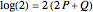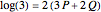Vega's Calculations of Logarithms

Initializing live version

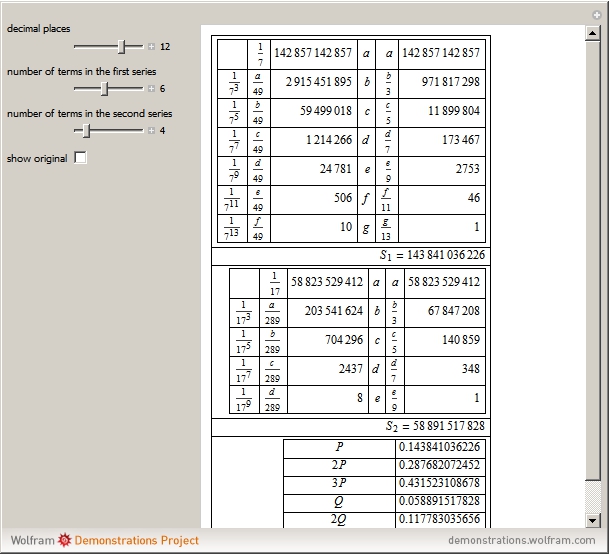
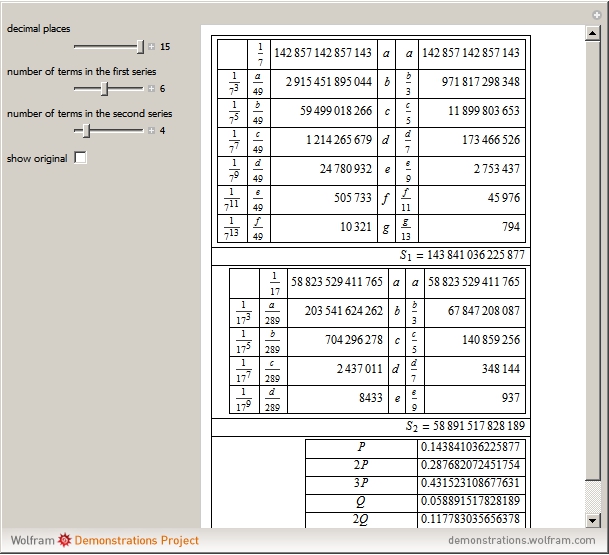
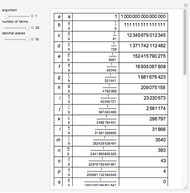
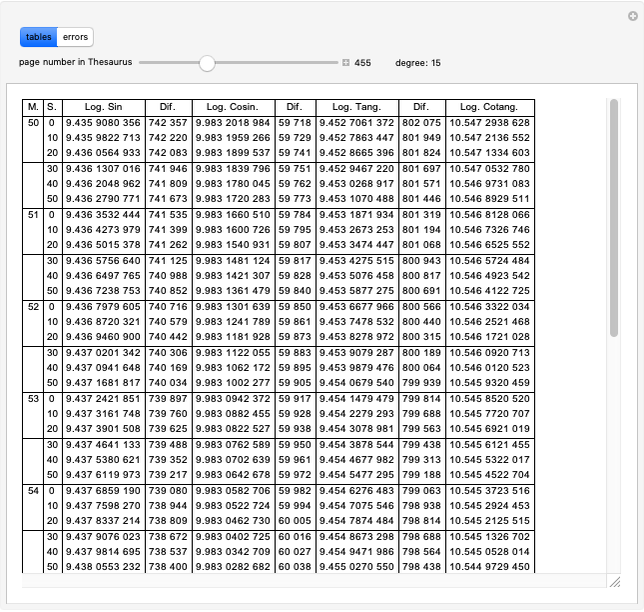
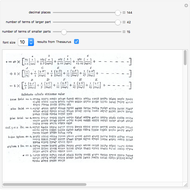
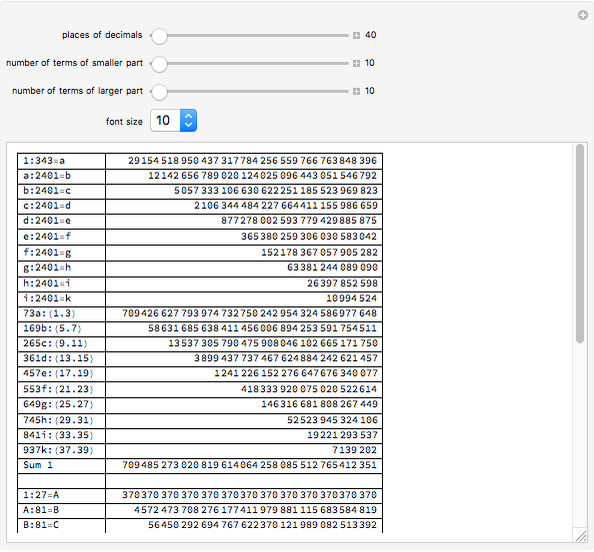
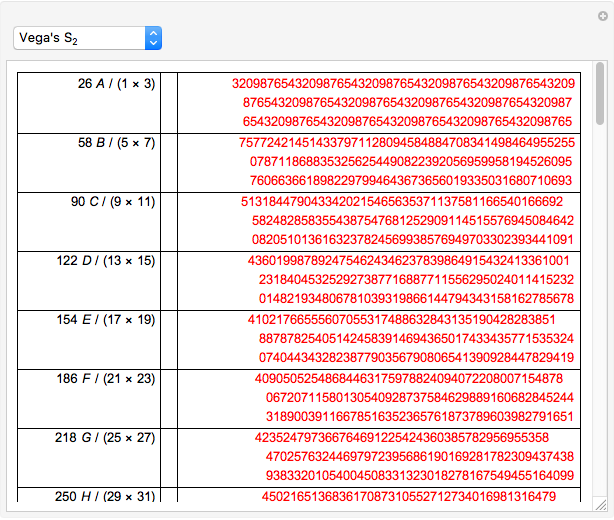
In the Thesaurus Logarithmorum, Vega calculate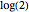d and 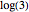using the formula

Contributed by: Izidor Hafner (November 2013)
Open content licensed under CC BY-NC-SA

Snapshots

In [1], 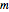is the factor for transforming common-to-natural logarithms. Check "show original" to compare the original source with this reconstruction.

Reference

[1] G. Vega, Thesaurus Logarithmorum, Leipzig, Germany: in libraria Wiedmannia, 1794 pp. v–vi.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send