Velocity Profile for Immiscible Viscous Fluids

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
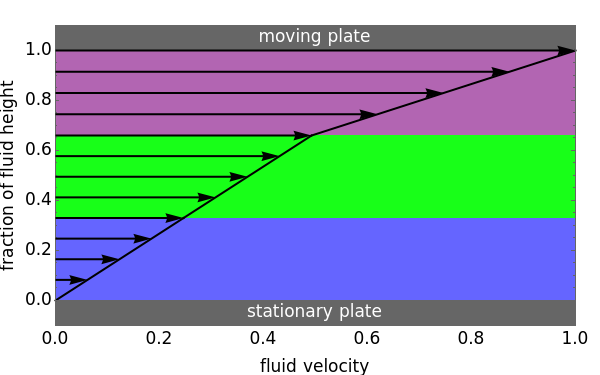
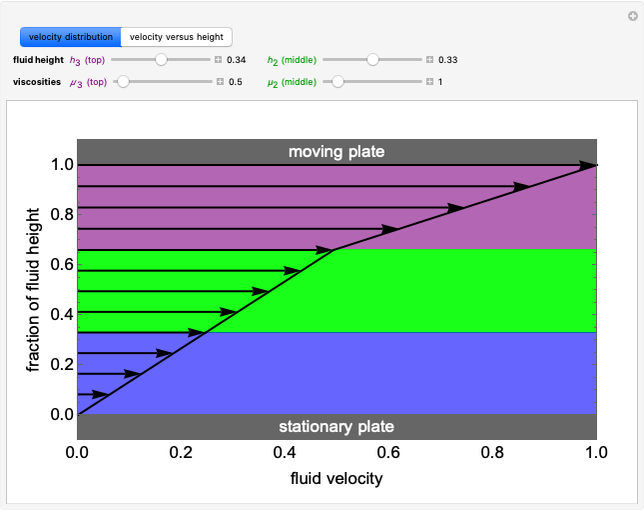
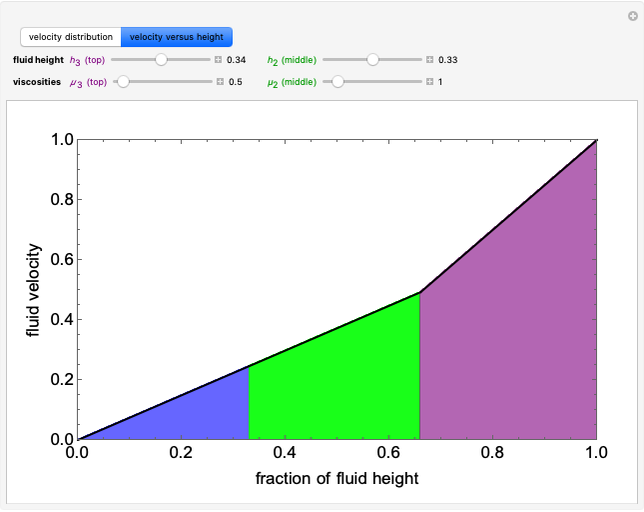
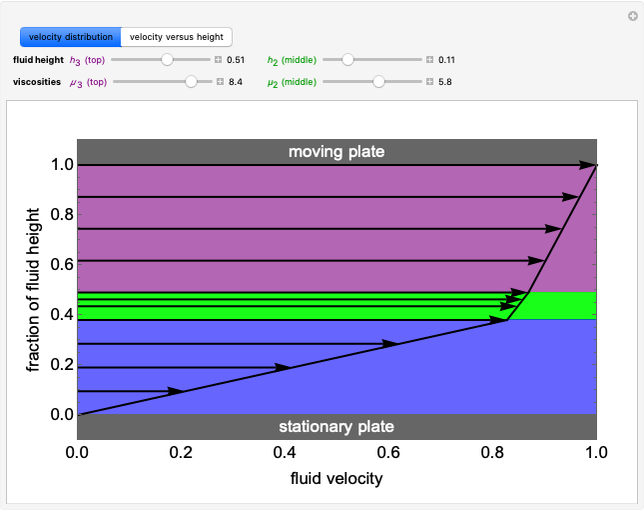
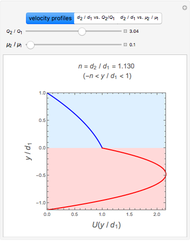
This Demonstration shows the behavior of three immiscible, incompressible fluids in laminar flow. The fluids are layered vertically and subjected to steady-state Couette flow; the top plate moves to the right at a constant velocity, and the bottom plate is stationary. At each height, the black arrow is proportional to the velocity of the fluid at that height. You can change the viscosities and heights of fluids 2 and 3 with sliders. The velocity distribution shows the impact of fluid viscosity on the fluid's velocity gradient. The velocity versus height plot indicates the relative slopes (or velocity gradients) in each fluid. All numbers are dimensionless.
Contributed by: Duncan Chadly, Michael Wrobel, Terra Salamida andRachael L. Baumann (December 2013)
Additional contributions by: Garret D. Nicodemus
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Couette flow is fluid flow through parallel plates where one plate is stationary and the other is moving at a constant velocity. In this Demonstration, the flow is at steady-state and fully developed. The Navier–Stokes equations in the 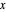 and
and 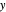 directions are used:
directions are used:
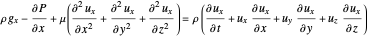 ,
,
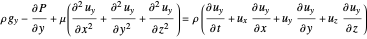 .
.
Since flow is steady-state and there is no flow in the  direction, these equations simplify to:
direction, these equations simplify to:
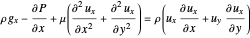 ,
,
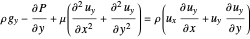 .
.
Flow is in the 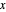 direction, so
direction, so  drops out:
drops out:
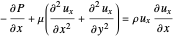 ,
,
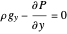 .
.
Since the flow is fully developed the velocity in the direction of flow does not change. It is assumed that the pressure is hydrostatic so pressure does not vary in the 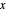 direction:
direction:
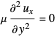 ,
,
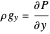 .
.
For the boundary conditions 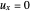 at
at 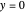 and
and 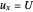 at
at 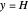 , the simplified Navier–Stokes equation is:
, the simplified Navier–Stokes equation is:
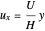 ,
,
where  is density,
is density, 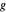 is gravity,
is gravity, 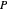 is pressure,
is pressure,  is viscosity,
is viscosity,  is fluid velocity,
is fluid velocity, 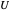 is plate velocity,
is plate velocity,  is time and
is time and 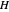 is the distance between plates.
is the distance between plates.
Reference
[1] B. R. Munson, T. H. Okiishi, and W. W. Huebsch, Fundamentals of Fluid Mechanics, 6th ed., Hoboken, NJ: John Wiley & Sons, 2010.
Permanent Citation