Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Vibrations of a Hanging String

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

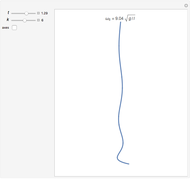
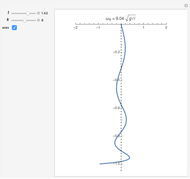
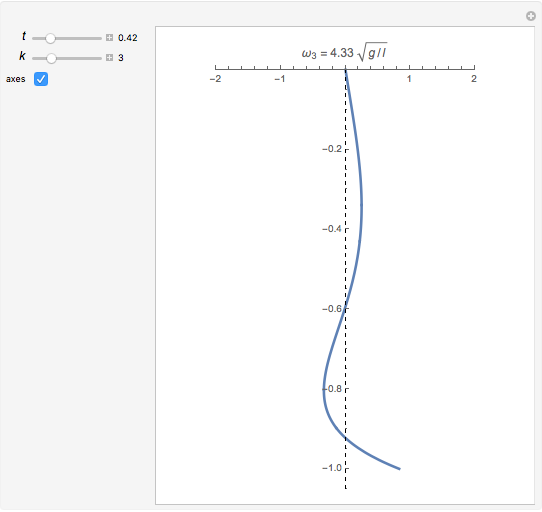
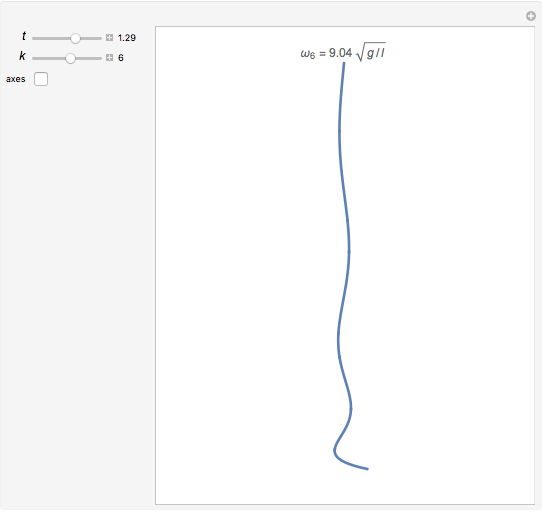
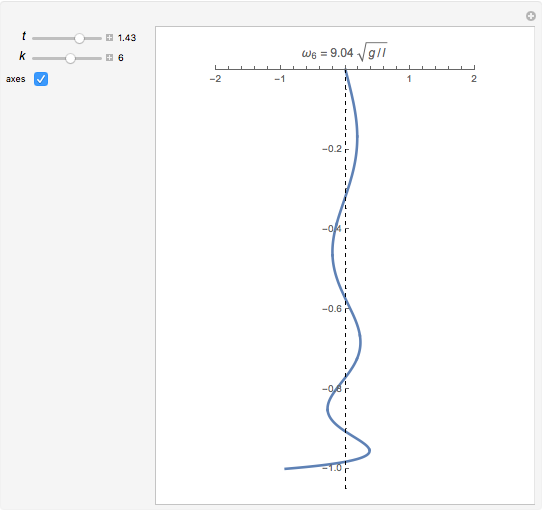
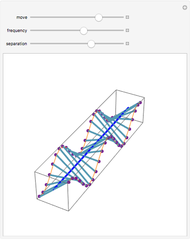
This Demonstration plots the vibrational mode of a freely hanging string, with horizontal amplitude given by

[more]

.

The label at the top of the plot gives the frequency of the mode selected by the second slider.

[less]

Contributed by: Enrique Zeleny (September 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The general solution for the vibrational problem is

,

with for , where is the length of the string, is the gravitational acceleration, and is the zero-order Bessel function of the first kind; the are the eigenfunctions. Only one term of the expansion, for a single value of , is plotted. The constants and 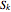are chosen here to be 1 and 0, respectively.

Reference

[1] P. Hagedorn and A. DasGupta, Vibrations and Waves in Continuous Mechanical Systems, Chichester, England: John Wiley & Sons, 2007.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send