Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Villarceau Circles

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

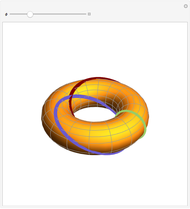
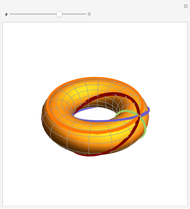
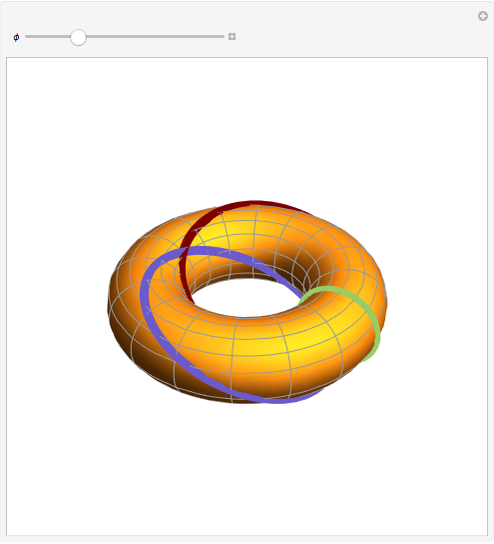
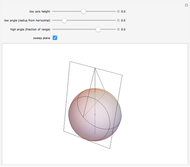
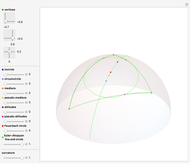
It is obvious that every point on a torus is contained in two circles that lie on the torus. Less obvious is the fact that every such point is contained in two additional circles, called the Villarceau circles.

Contributed by: Stan Wagon (Macalester College) (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This code is taken from S. Wagon, Mathematica in Action, 3rd ed., forthcoming from Springer-Verlag.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send