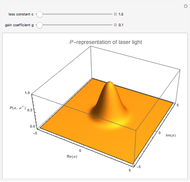
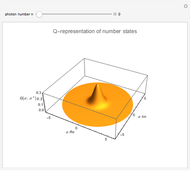
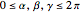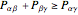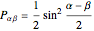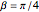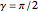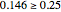Violation of Bell's Inequality: A Confirmation of Quantum Theory

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
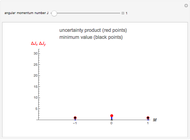
In Bohm's reformulation of the Einstein–Podolsky–Rosen experiment a spin-zero particle decays into two spin (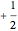 ,
, 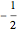 ) particles moving in opposite directions. The particles are detected by two polarization filters (Stern–Gerlach devices, SG1 and SG2) oriented by an angle
) particles moving in opposite directions. The particles are detected by two polarization filters (Stern–Gerlach devices, SG1 and SG2) oriented by an angle  (for particle 1) and an angle
(for particle 1) and an angle 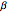 (for particle 2) with respect to the vertical (positive
(for particle 2) with respect to the vertical (positive  ) direction. Two counters register spin (+
) direction. Two counters register spin (+ ) particles only.
) particles only.
Contributed by: Reinhard Tiebel (May 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
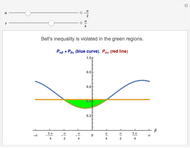
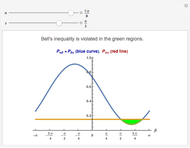
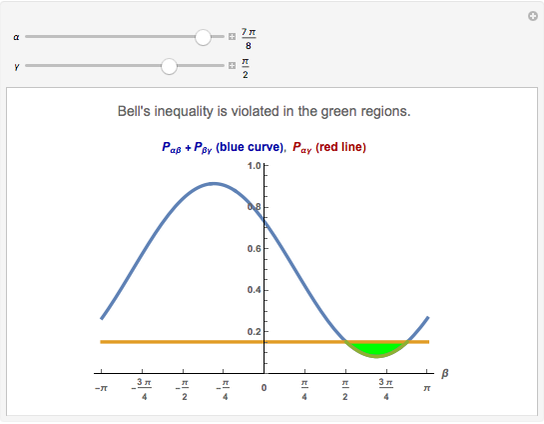
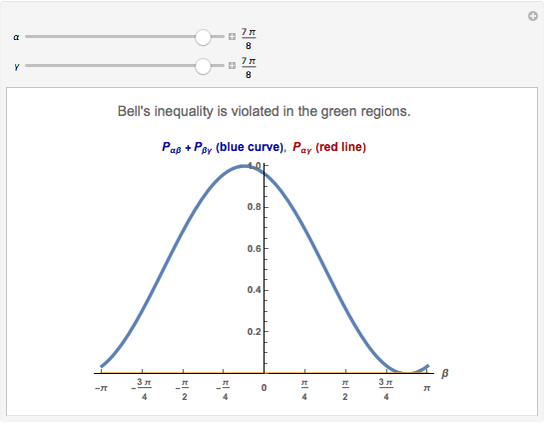
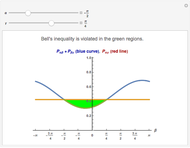
Quantum mechanics does not make definite predictions for the outcome of measurements. If the actual state of the physical system is known, then probabilities for the possible measurements can be calculated. For many natural scientists it is difficult to accept that in an experiment a definite final state is chosen from among all the possible outcomes. The quantum theory seems to be incomplete.
Thus some people have tried to make the quantum theory "complete" and "deterministic" with the help of the inclusion "hidden variables" in the theoretical description. Bell's inequality is an expression of expected classical results. There are some different versions of Bell's inequality related to the one shown here. All experimental results on two-photon correlations thus far [4] have shown violations of Bell's inequality. A tentative conclusion from these results has been summarized as "Bell's theorem": No physical theory of local hidden variables can ever reproduce all the predictions of quantum mechanics. There still remain, however, a number of unlikely but possible philosophical loopholes that have been evoked in counterarguments.
References
[1] M. O. Scully and M. S. Zubairy, Quantum Optics, Cambridge: Cambridge University Press, 1997.
[2] F. Schwabl, Quantenmechanik, Berlin Heidelberg: Springer–Verlag, 1993.
[3] J. Audretsch, Verschränkte Systeme—Die Quantenphysik auf neuen Wegen, Berlin: Wiley-VCH, 2005.
[4] A. Aspect, J. Dalibard, and G. Roger, "Experimental Test of Bell's Inequalities Using Time-Varying Analyzers, Physical Review Letters 49, 1982 pp. 1804–1807.
Permanent Citation