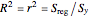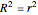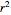Visualizing R-Squared in Statistics
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
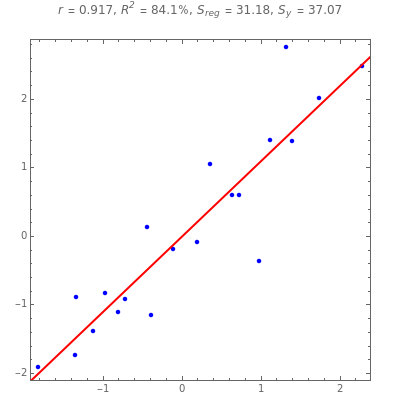
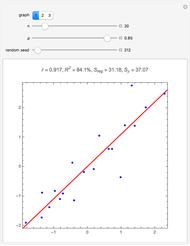
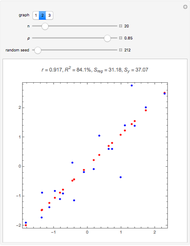
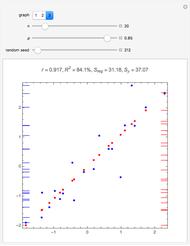
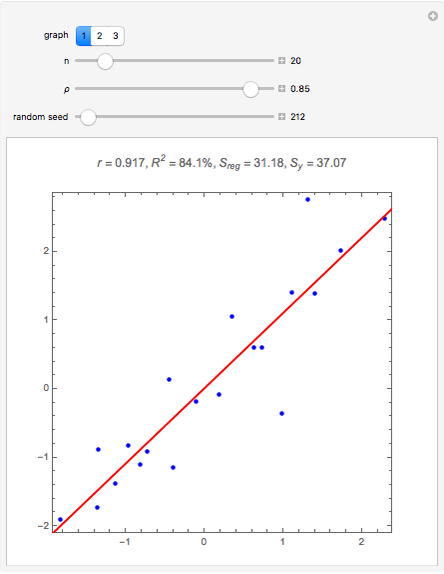
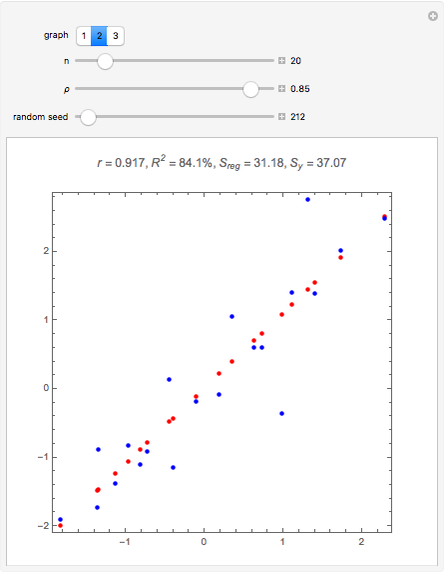
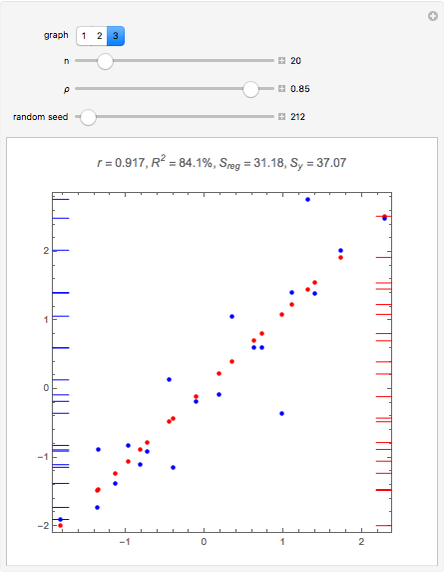
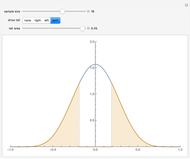
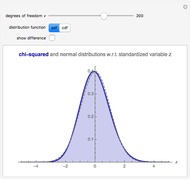
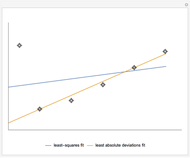
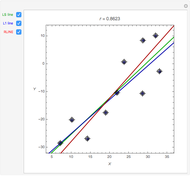
In general, 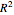 is often referred to as the coefficient of determination and its verbal interpretation is that it is the fraction of variation explained by the model. This in fact is illustrated in our Demonstration in the case of simple linear regression.
is often referred to as the coefficient of determination and its verbal interpretation is that it is the fraction of variation explained by the model. This in fact is illustrated in our Demonstration in the case of simple linear regression.
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation