Volpert Graph of Chemical Reactions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
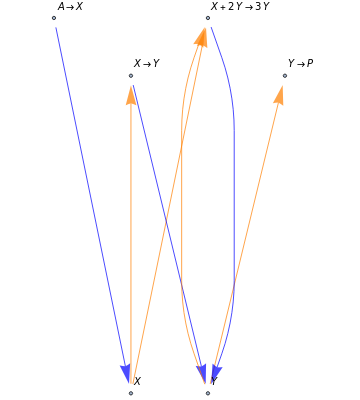
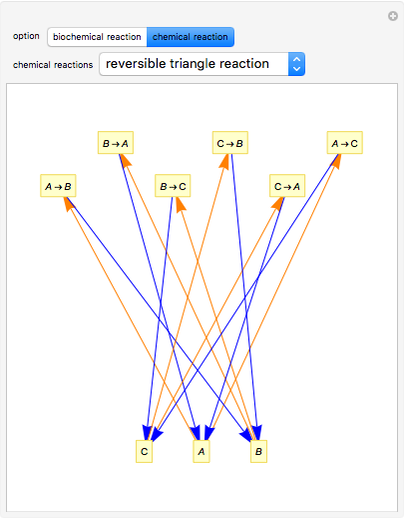
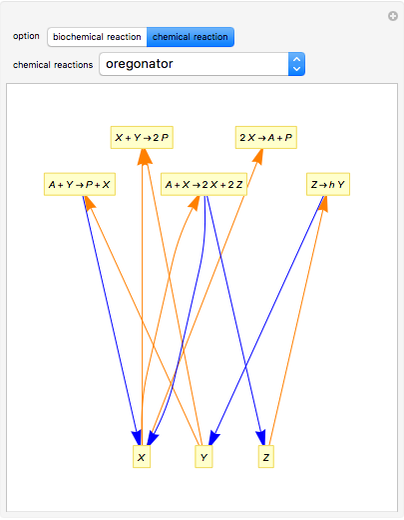
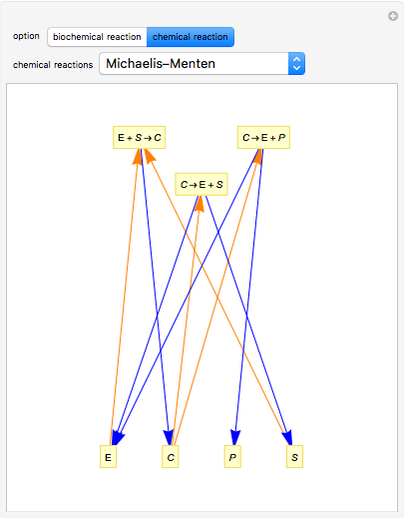
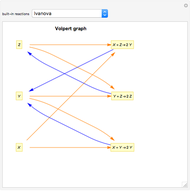
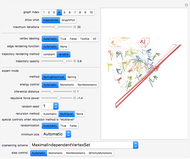
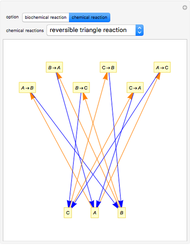
In reaction network theory, the Volpert graph is a directed bipartite graph whose vertex sets are the chemical species and the reaction steps. There is an edge from a species to a reaction step if and only if the reactant complex of the reaction step contains the species, and there is an edge from a reaction step to a species if and only if the product complex of the reaction step contains the species. The Volpert graph turns out to be very important in theory and it corresponds to the definition of the graphs used by biochemists.
Contributed by: Attila Nagy (March 2011)
Suggested by: János Tóth
Open content licensed under CC BY-NC-SA
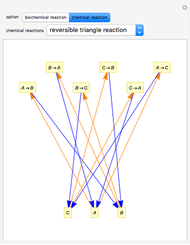
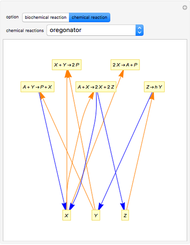
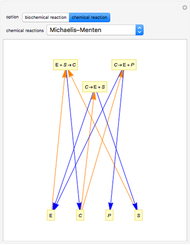
Snapshots
Details
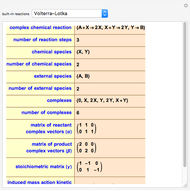
The Volpert graph of the formal reaction mechanism 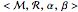 is the directed bipartite graph:
is the directed bipartite graph: 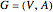 , where the vertex set
, where the vertex set 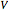 is the set
is the set 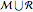 , and
, and 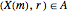 , iff
, iff 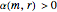 , and
, and 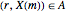 , iff
, iff 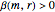 , where
, where 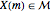 and
and 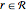 . There is no directed edge either inside
. There is no directed edge either inside 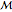 or inside
or inside 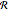 .
.
The Demonstration can also be used to analyze any other type of reaction. For more information about the formal reaction mechanism see the Descriptive Reaction Kinetics Demonstration.
P. Érdi and J. Tóth: Mathematical Models of Chemical Reactions: Theory and Applications of Deterministic and Stochastic Models, Princeton: Princeton University Press, 1989.
Permanent Citation
"Volpert Graph of Chemical Reactions"
http://demonstrations.wolfram.com/VolpertGraphOfChemicalReactions/
Wolfram Demonstrations Project
Published: March 7 2011