Volume and Mass of a Spoonful of Powder

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
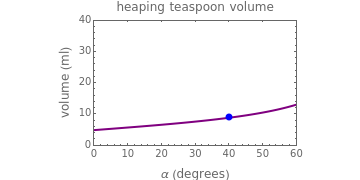
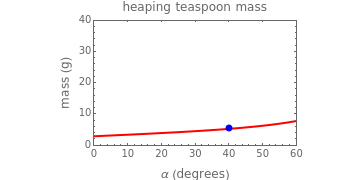
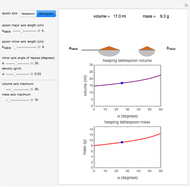
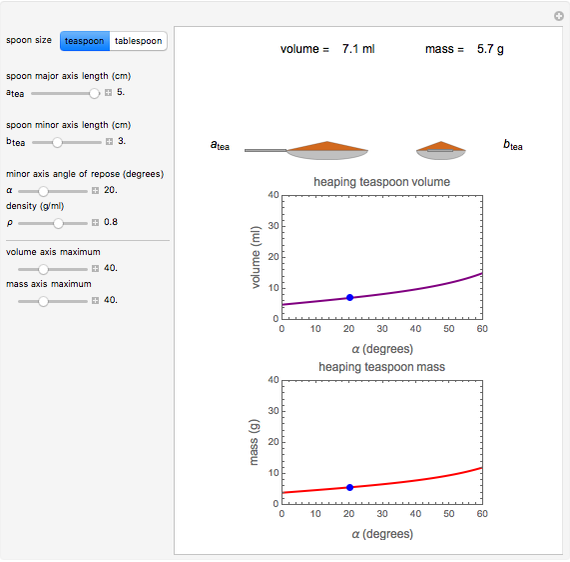
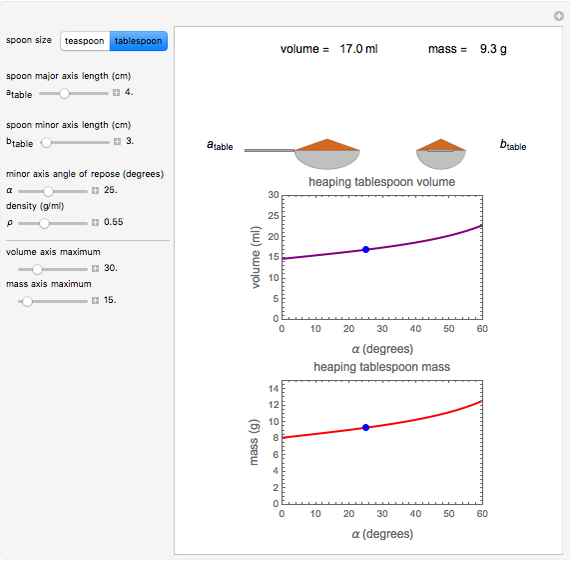
This Demonstration calculates the volume and mass of a powder resting on a teaspoon or tablespoon as a function of the spoon's shape and size, the powder's angle of repose, and the powder's bulk density. The Demonstration is based on the standard volume of a teaspoon being about 4.9 ml and a tablespoon 14.8 ml. The calculated values are for idealized spoons having hemispheric or ellipsoidal shapes and heaps with smooth surfaces.
Contributed by: Mark D. Normand and Micha Peleg (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: oval-shaped teaspoonful of free-flowing powder
Snapshot 2: oval-shaped tablespoonful of cohesive powder
Snapshot 3: oval-shaped tablespoonful of free-flowing powder
Snapshot 4: circular-shaped level tablespoonful of powder
This Demonstration calculates the volume and mass of a powder with or without a heap resting in an idealized teaspoon or tablespoon. We assume that the spoon has either a hemispheric shape, as in measuring spoons, or an ellipsoidal shape reminiscent of common spoons. We also assume that the heap, when present, has a smooth surface.
Choose a spoon type with the setter bar. The calculation parameters, all entered with sliders, are: the spoon's major and minor axis lengths,  and
and  , respectively, the powder's minor axis angle of repose,
, respectively, the powder's minor axis angle of repose,  , in degrees, and its bulk density,
, in degrees, and its bulk density,  , in g/ml.
, in g/ml.
The program displays the calculated numerical value of the powder's volume, in ml, and mass, in g, with a schematic diagram of the spoon and powder for the chosen parameters (not to scale). The program also displays corresponding plots of the spoon's volume and mass against the powder's angle of repose on which the chosen settings are marked with a blue dot. The upper limits of the  axes for both plots can be adjusted by the user with sliders.
axes for both plots can be adjusted by the user with sliders.
Note that in very cohesive powders, which exhibit a high angle of repose, it is unlikely that the heap's shape would be smooth.
Reference
[1] M. Peleg, "Physical Characteristics of Food Powders," in Physical Properties of Foods (M. Peleg and E. B. Bagley, eds.), Westport, CT: AVI, Inc., 1983 pp. 293–323.
Permanent Citation