Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

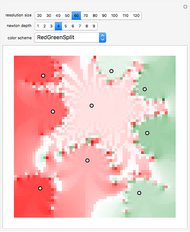
Wallpaper Patterns Generated by Complex Mapping of a Picture

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

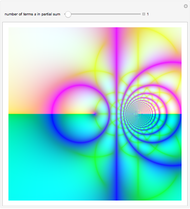
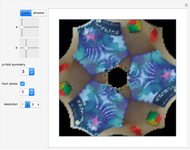
One way of visualizing a complex-valued function 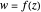in the plane is to assign a unique color to each point of a certain region of the complex plane—for example, the color value on a picture of the point with coordinates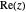 and . In this way, wallpaper patterns can be produced.

[more]

Since producing these graphics might be slow, it is recommended that you first construct small pictures at low resolution.

[less]

Contributed by: Izidor Hafner (February 2016)
(Idea by Frank A. Farris)
Open content licensed under CC BY-NC-SA

Snapshots

Details

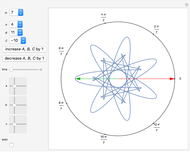
Let 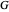be a finite group of 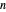rotational transformations in the complex plane. 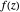is a function defined on the complex plane. An average of 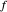over can be defined by

.

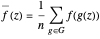For example, in the case 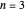we can choose the group .

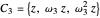This Demonstration considers also the cases for rotations of order 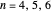. No periodic wallpaper pattern can be produced for .

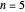Reference

[1] F. A. Farris, Creating Symmetry: The Artful Mathematics of Wallpaper Patterns, Princeton: Princeton University Press, 2015 pp. 66–67.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send