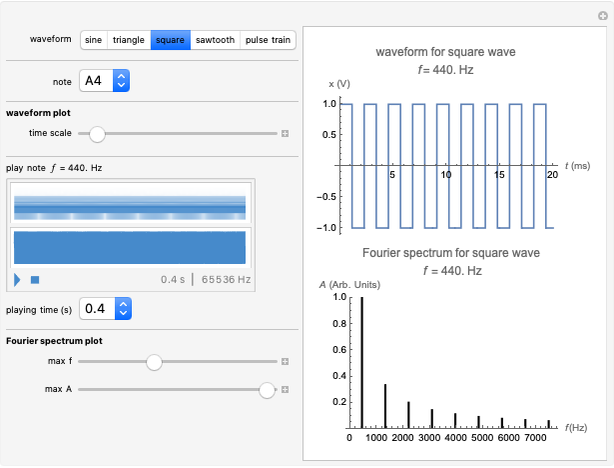
Waveforms and Spectrograms

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
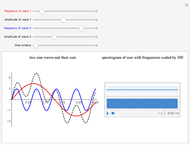
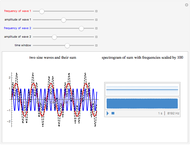
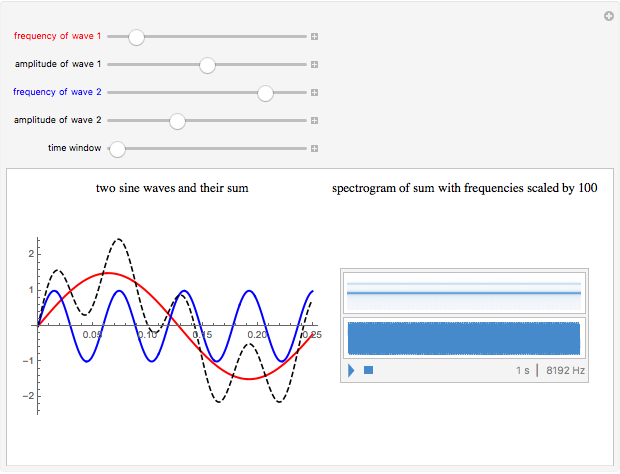
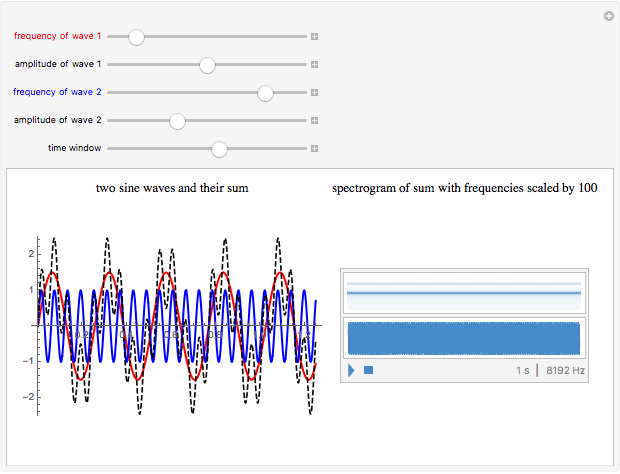
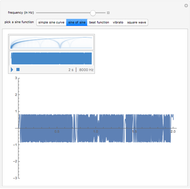
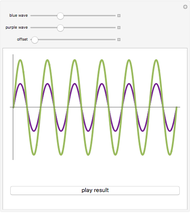
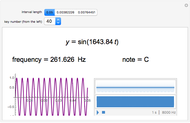
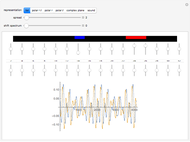
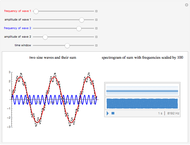
Change the amplitude and frequency of the two component sine waves to create a complex, non-sinusoidal wave (dashed). On the right of the display, you see a spectrogram above a waveform, one second in duration. The location of bars in the spectrogram changes as you adjust the frequencies. To create this spectrogram display and the linked sound, the frequencies of wave 1 and wave 2 are multiplied by 100, in order to bring them into the range of human hearing.
Contributed by: Charles Reiss (Concordia University, Montreal) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
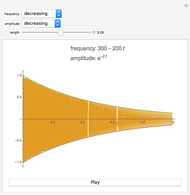
The left illustrates how adding two sine waves of various amplitudes and frequencies (from 1 to 20Hz) creates complex waves (in dashed black). On the right, a spectrogram display illustrates the fact that a complex wave can be analyzed into its sinusoidal components. Observe the bands in the spectrogram as you change the frequencies of the component waves. Changing the amplitude also affects the appearance of the spectrogram—can you see how? The spectrogram plots time on the  axis and frequency on the
axis and frequency on the 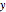 axis. Dark regions show relative energy at a given frequency. The spectrogram shows the original sinusoidal components of the created wave as horizontal bands. Fourier analysis allows any complex wave to be expressed as a combination of sinusoidal (sine and cosine) waves. The distribution of bands in the spectrogram reflects the quality of sounds that may otherwise share the same duration, loudness, and basic pitch. Differences in the timbre of instruments playing the same note and differences among vowel sounds correspond to variations in the distribution of energy across the frequency spectrum.
axis. Dark regions show relative energy at a given frequency. The spectrogram shows the original sinusoidal components of the created wave as horizontal bands. Fourier analysis allows any complex wave to be expressed as a combination of sinusoidal (sine and cosine) waves. The distribution of bands in the spectrogram reflects the quality of sounds that may otherwise share the same duration, loudness, and basic pitch. Differences in the timbre of instruments playing the same note and differences among vowel sounds correspond to variations in the distribution of energy across the frequency spectrum.
Fourier Analysis and Synthesis: http://hyperphysics.phy-astr.gsu.edu/hbase/audio/Fourier.html
Permanent Citation
"Waveforms and Spectrograms"
http://demonstrations.wolfram.com/WaveformsAndSpectrograms/
Wolfram Demonstrations Project
Published: March 7 2011