Why a Number Is Prime
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
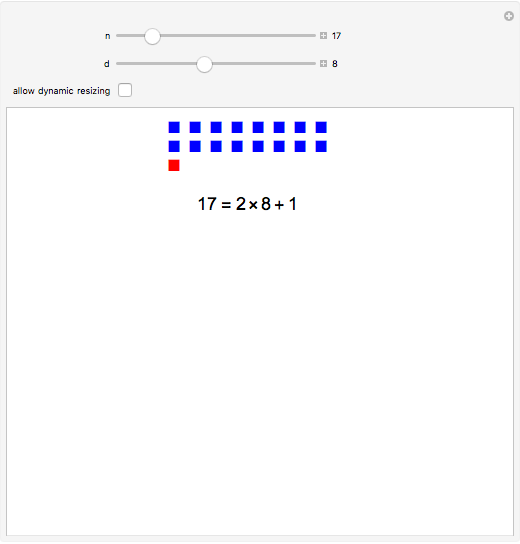
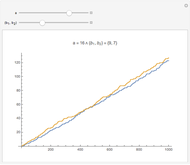
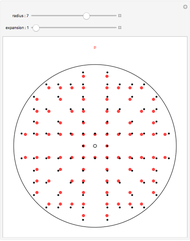
Move the  slider to see that if
slider to see that if  is a prime number,
is a prime number,  squares cannot be arranged into a rectangular array unless the width or length is 1. That is, it is not possible to represent a prime as the product of two integers
squares cannot be arranged into a rectangular array unless the width or length is 1. That is, it is not possible to represent a prime as the product of two integers  with
with  .
.
Contributed by: Enrique Zeleny (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation